
【题目】函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)图象的一部分如图所示,函数g(x)=f(x+ ![]() ),则下列结论正确的是( )
),则下列结论正确的是( ) 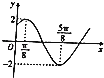
A.函数g(x)的奇函数
B.函数f(x)与g(x)的图象均关于直线x=﹣ ![]() π对称
π对称
C.函数f(x)与g(x)的图象均关于点(﹣ ![]() ,0)对称
,0)对称
D.函数f(x)与g(x)在区间(﹣ ![]() ,0)上均单调递增
,0)上均单调递增
【答案】D
【解析】解:根据函数f(x)的图象知,A=2; ![]() =
= ![]() ﹣
﹣ ![]() =
= ![]() ,∴T=π,ω=
,∴T=π,ω= ![]() =2;
=2;
2× ![]() +φ=
+φ= ![]() ,φ=
,φ= ![]() ;
;
∴f(x)=2sin(2x+ ![]() );
);
函数g(x)=f(x+ ![]() )=2sin[2(x+
)=2sin[2(x+ ![]() )+
)+ ![]() ]=2cos2x;
]=2cos2x;
由此得函数g(x)不是定义域R上的奇函数,A错误;
由f(﹣ ![]() )=2sin(﹣
)=2sin(﹣ ![]() π+
π+ ![]() )=2,函数f(x)关于x=﹣
)=2,函数f(x)关于x=﹣ ![]() 对称,
对称,
g(﹣ ![]() )=2cos(﹣
)=2cos(﹣ ![]() )=
)= ![]() ,函数g(x)不关于x=﹣
,函数g(x)不关于x=﹣ ![]() 对称,B错误;
对称,B错误;
由f(﹣ ![]() )=2sin(﹣
)=2sin(﹣ ![]() +
+ ![]() )=﹣
)=﹣ ![]() ,函数不关于(﹣
,函数不关于(﹣ ![]() ,0)对称,C错误;
,0)对称,C错误;
由x∈(﹣ ![]() ,0),2x+
,0),2x+ ![]() ∈(﹣
∈(﹣ ![]() ,
, ![]() ),函数f(x)=2sin(2x+
),函数f(x)=2sin(2x+ ![]() )是单调增函数,
)是单调增函数,
2x∈(﹣ ![]() ,0),g(x)=2cos2x是单调增函数,D正确.
,0),g(x)=2cos2x是单调增函数,D正确.
故选:D.


科目:高中数学 来源: 题型:
【题目】以下数表的构造思路源于我国南宋数学家杨辉所著的《详解九章算术》一书中的“杨辉三角性”. 
该表由若干行数字组成,从第二行起,每一行中的数字均等于其“肩上”两数之和,表中最后一行仅有一个数,则这个数为( )
A.2017×22015
B.2017×22014
C.2016×22015
D.2016×22014
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三人准备报考某大学,假设甲考上的概率为 ![]() ,甲,丙两都考不上的概率为
,甲,丙两都考不上的概率为 ![]() ,乙,丙两都考上的概率为
,乙,丙两都考上的概率为 ![]() ,且三人能否考上相互独立.
,且三人能否考上相互独立.
(1)求乙、丙两人各自考上的概率;
(2)设X表示甲、乙、丙三人中考上的人数与没考上的人数之差的绝对值,求X的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图已知四棱锥P﹣ABCD的底面ABCD是边长为2的正方形,PD⊥底面ABCD,E,F分别为棱BC,AD的中点. 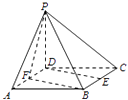
(1)若PD=1,求异面直线PB和DE所成角的余弦值.
(2)若二面角P﹣BF﹣C的余弦值为 ![]() ,求四棱锥P﹣ABCD的体积.
,求四棱锥P﹣ABCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,⊙O是等腰三角形ABC的外接圆,AB=AC,延长BC到点D,使CD=AC,连接AD交⊙O于点E,连接BE与AC交于点F. 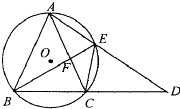
(1)判断BE是否平分∠ABC,并说明理由;
(2)若AE=6,BE=8,求EF的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=﹣x3+ax在(﹣1,0)上是增函数.
(1)求实数a的取值范围A;
(2)当a为A中最小值时,定义数列{an}满足:a1∈(﹣1,0),且2an+1=f(an),用数学归纳法证明an∈(﹣1,0),并判断an+1与an的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为感谢全体员工的辛勤劳动,决定在年终答谢会上,通过摸球方式对全公司1000位员工进行现金抽奖。规定:每位员工从装有4个相同质地球的袋子中一次性随机摸出2个球,这4个球上分别标有数字![]() 、
、![]() 、
、![]() 、
、![]() ,摸出来的两个球上的数字之和为该员工所获的奖励额
,摸出来的两个球上的数字之和为该员工所获的奖励额![]() (单位:元)。公司拟定了以下三个数字方案:
(单位:元)。公司拟定了以下三个数字方案:
方案 |
|
|
|
|
一 | 100 | 100 | 100 | 500 |
二 | 100 | 100 | 500 | 500 |
三 | 200 | 200 | 400 | 400 |
(Ⅰ)如果采取方案一,求![]() 的概率;
的概率;
(Ⅱ)分别计算方案二、方案三的平均数![]() 和方差
和方差![]() ,如果要求员工所获的奖励额相对均衡,方案二和方案三选择哪个更好?
,如果要求员工所获的奖励额相对均衡,方案二和方案三选择哪个更好?
(Ⅲ)在投票选择方案二还是方案三时,公司按性别分层抽取100名员工进行统计,得到如下不完整的![]() 列联表。请将该表补充完整,并判断能否有90%的把握认为“选择方案二或方案三与性别有关”?
列联表。请将该表补充完整,并判断能否有90%的把握认为“选择方案二或方案三与性别有关”?
方案二 | 方案三 | 合计 | |
男性 | 12 | ||
女性 | 40 | ||
合计 | 82 | 100 |
附:![]()
| 0.15 | 0.10 | 0.05 |
| 2.072 | 2.706 | 3.841 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com