
我国政府对PM2.5采用如下标准:
| PM2.5日均值m(微克/立方米) | 空气质量等级 |
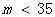 | 一级 |
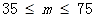 | 二级 |
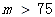 | 超标 |

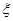 表示空气质量达到一级的天数,求
表示空气质量达到一级的天数,求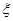 的分布列;
的分布列;(1)41;(2)分布列详见解析;(3)72.
解析试题分析:本题主要考查茎叶图、中位数、超几何分布、二项分布以及期望公式等基础知识,考查学生的分析问题解决问题的能力、计算能力.第一问,利用茎叶图计算中位数,将一组数据按从小到大的顺序排列,当数据有奇数个时,处在最中间的一个数是这组数据的中位数;第二问,利用超几何分布的计算公式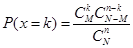 计算每种情况的概率,再列出分布列;第三问,在10天中,
计算每种情况的概率,再列出分布列;第三问,在10天中,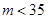 的有4天,所以每天空气质量达到一级的概率为
的有4天,所以每天空气质量达到一级的概率为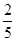 ,利用二项分布,利用
,利用二项分布,利用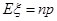 直接计算数学期望.
直接计算数学期望.
试题解析:(1)10天的中位数为(38+44)/2=41(微克/立方米) 2分
(2)由 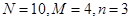 ,
,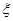 的可能值为0,1,2,3
的可能值为0,1,2,3
利用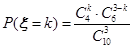
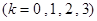 即得分布列:
即得分布列: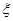
0 1 2 3 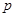
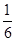
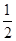
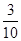
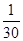
(3)一年中每天空气质量达到一级的概率为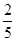 ,由
,由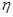 ~
~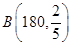 , 得到
, 得到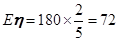 (天) ,
(天) ,
一年中空气质量达到一级的天数为72天. 13分
考点:茎叶图、中位数、超几何分布、二项分布以及期望公式.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:高中数学 来源: 题型:解答题
甲乙两人各有 个材质、大小、形状完全相同的小球,甲的小球上面标有
个材质、大小、形状完全相同的小球,甲的小球上面标有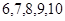 五个数字,乙的小球上面标有
五个数字,乙的小球上面标有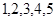 五个数字.把各自的小球放入两个不透明的口袋中,两人同时从各自的口袋中随机摸出
五个数字.把各自的小球放入两个不透明的口袋中,两人同时从各自的口袋中随机摸出 个小球.规定:若甲摸出的小球上的数字是乙摸出的小球上的数字的整数倍,则甲获胜,否则乙获胜.
个小球.规定:若甲摸出的小球上的数字是乙摸出的小球上的数字的整数倍,则甲获胜,否则乙获胜.
(1)写出基本事件空间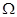 ;
;
(2)你认为“规定”对甲、乙二人公平吗?说出你的理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校从高一年级周末考试的学生中抽出6O名学生,其成绩(均为整数)的频率分布直方图如图所示:(1)依据频率分布直方图,估计这次考试的及格率(60分及以上为及格)和平均分;(2)已知在[90,100]段的学生的成绩都不相同,且都在94分以上,现用简单随机抽样方法,从95,96,97,98,99,100这6个数中任取2个数,求这2个数恰好是两个学生的成绩的概率.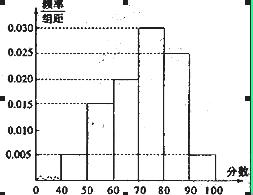
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,某中学甲、乙两班共有25名学生报名参加了一项 测试.这25位学生的考分编成的茎叶图,其中有一个数据因电脑操作员不小心删掉了(这里暂用x来表示),但他清楚地记得两班学生成绩的中位数相同.
(1)求这两个班学生成绩的中位数及x的值;
(2)如果将这些成绩分为“优秀”(得分在175分以上,包括175分)和“过关”,若学校再从这两个班获得“优秀”成绩的考生中选出3名代表学校参加比赛,求这3人中甲班至多有一人入选的概率.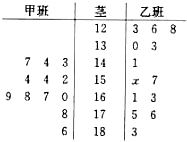
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
袋中装有编号为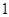 的球
的球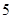 个,编号为
个,编号为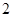 的球
的球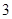 个,这些球的大小完全一样。
个,这些球的大小完全一样。
(1)从中任意取出四个,求剩下的四个球都是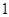 号球的概率;
号球的概率;
(2)从中任意取出三个,记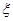 为这三个球的编号之和,求随机变量
为这三个球的编号之和,求随机变量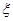 的分布列及其数学期望
的分布列及其数学期望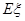 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知 、
、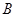 两盒中都有红球、白球,且球的形状、大小都相同,盒子
两盒中都有红球、白球,且球的形状、大小都相同,盒子 中有
中有 个红球与
个红球与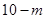 个白球,盒子
个白球,盒子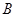 中有
中有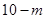 个红球与
个红球与 个白球(
个白球(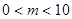 ).
).
(1)分别从 、
、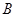 中各取一个球,
中各取一个球, 表示红球的个数;
表示红球的个数;
①请写出随机变量 的分布列,并证明
的分布列,并证明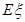 等于定值;
等于定值;
②当 为何值时,
为何值时,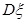 取到最小值,并求出最小值.
取到最小值,并求出最小值.
(2)在盒子 中不放回地摸取3个球,事件
中不放回地摸取3个球,事件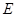 :在第一次取到红球后,以后两次都取到白球,事件
:在第一次取到红球后,以后两次都取到白球,事件 :在第一次取到白球后,以后两次都取到红球,若概率
:在第一次取到白球后,以后两次都取到红球,若概率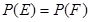 ,求
,求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(13分)(2011•重庆)某市公租房的房源位于A、B、C三个片区,设每位申请人只申请其中一个片区的房源,且申请其中任一个片区的房源是等可能的,求该市的任4位申请人中:
(Ⅰ)恰有2人申请A片区房源的概率;
(Ⅱ)申请的房源所在片区的个数的ξ分布列与期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某示范性高中的校长推荐甲、乙、丙三名学生参加某大学自主招生考核测试,在本次考核中只有合格和优秀两个等级.若考核为合格,授予10分降分资格;考核为优秀, 授予20分降分资格.假设甲、乙、丙考核为优秀的概率分别为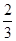 、
、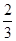 、
、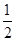 ,他们考核所得的等级相互独立.
,他们考核所得的等级相互独立.
(1)求在这次考核中,甲、乙、丙三名学生至少有一名考核为优秀的概率;
(2)记在这次考核中甲、乙、丙三名学生所得降分之和为随机变量ξ,求随机变量ξ的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com