
【题目】已知集合A={x| ![]() <2x<4},B={x|0<log2x<2}.
<2x<4},B={x|0<log2x<2}.
(1)求A∩B和A∪B;
(2)记M﹣N={x|x∈M,且xN},求A﹣B与B﹣A.
【答案】
(1)解:集合A={x| ![]() <2x<4}={x|﹣1<x<2},
<2x<4}={x|﹣1<x<2},
B={x|0<log2x<2}={x|0<x<4};
A∩B={x|0<x<2},
A∪B={x|﹣1<x<4}
(2)解:记M﹣N={x|x∈M,且xN},
则A﹣B={x|﹣1<x≤0},
B﹣A={x|2≤x<4}
【解析】(1)化简集合A、B,根据交集与并集的定义写出A∩B和A∪B;(2)根据M﹣N的定义,写出A﹣B与B﹣A即可.
【考点精析】本题主要考查了交、并、补集的混合运算的相关知识点,需要掌握求集合的并、交、补是集合间的基本运算,运算结果仍然还是集合,区分交集与并集的关键是“且”与“或”,在处理有关交集与并集的问题时,常常从这两个字眼出发去揭示、挖掘题设条件,结合Venn图或数轴进而用集合语言表达,增强数形结合的思想方法才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,已知位于y轴左侧的圆C与y轴相切于点(0,1)且被x轴分成的两段圆弧长之比为1:2,过点H(0,t)的直线l于圆C相交于M、N两点,且以MN为直径的圆恰好经过坐标原点O. 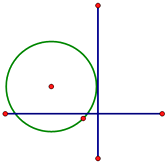
(1)求圆C的方程;
(2)当t=1时,求出直线l的方程;
(3)求直线OM的斜率k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300)分组的频率分布直方图如图. 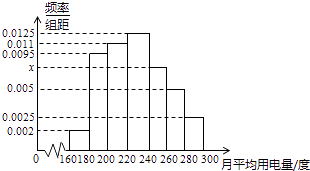
(1)求直方图中x的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为,[220,240),[240,260),[260,280),[280,300)的四组用户中,用分层抽样的方法抽取11户居民,则月平均用电量在[220,240)的用户中应抽取多少户?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某毕业生参加人才招聘会,分别向甲、乙、丙三个公司投递了个人简历,假定该毕业生得到甲公司面试的概率为 ![]() ,得到乙公司和丙公司面试的概率均为p,且三个公司是否让其面试是相互独立的.记ξ为该毕业生得到面试的公司个数,若P(ξ=0)=
,得到乙公司和丙公司面试的概率均为p,且三个公司是否让其面试是相互独立的.记ξ为该毕业生得到面试的公司个数,若P(ξ=0)= ![]()
(Ⅰ)求p的值:
(Ⅱ)求随机变量ξ的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线x2=4y,圆C:x2+(y﹣2)2=4,点M(x0 , y0),(x0>0,y0>4)为抛物线上的动点,过点M的圆C的两切线,设其斜率分别为k1 , k2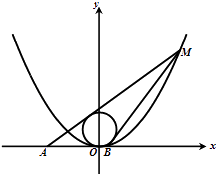
(Ⅰ)求证:k1+k2= ![]() ,k1k2=
,k1k2= ![]() .
.
(Ⅱ)求过点M的圆的两切线与x轴围成的三角形面积S的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1(﹣1,0),F2(1,0)是椭圆C1与双曲线C2共同的焦点,椭圆的一个短轴端点为B,直线F1B与双曲线的一条渐近线平行,椭圆C1与双曲线C2的离心率分别为e1 , e2 , 则e1+e2取值范围为( )
A.[2,+∞)
B.[4,+∞)
C.(4,+∞)
D.(2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某乐园按时段收费,收费标准为:每玩一次不超过1小时收费10元,超过1小时的部分每小时收费8元(不足1小时的部分按1小时计算).现有甲、乙二人参与但都不超过4小时,甲、乙二人在每个时段离场是等可能的.为吸引顾客,每个顾客可以参加一次抽奖活动.
(1)用(10,10)表示甲乙玩都不超过1小时的付费情况,求甲、乙二人付费之和为44元的概率;
(2)抽奖活动的规则是:顾客通过操作按键使电脑自动产生两个[0,1]之间的均匀随机数x,y,并按如图所示的程序框图执行.若电脑显示“中奖”,则该顾客中奖;若电脑显示“谢谢”,则不中奖,求顾客中奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,且经过点A(0,﹣1).
,且经过点A(0,﹣1).
(1)求椭圆C的标准方程;
(2)如果过点 ![]() 的直线与椭圆交于M,N两点(M,N点与A点不重合),求证:△AMN为直角三角形.
的直线与椭圆交于M,N两点(M,N点与A点不重合),求证:△AMN为直角三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com