
【题目】已知函数![]() ,
,![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若![]() 有两个极值点
有两个极值点![]() ,
,![]() ,且
,且![]() ,证明:
,证明:![]() .
.
【答案】(1)见解析.(2)见解析.
【解析】分析:(1)先求导数,再根据二次方程![]() =0根得情况分类讨论:当
=0根得情况分类讨论:当![]() 时,
时,![]() .∴
.∴![]() 在
在![]() 上单调递减. 当
上单调递减. 当![]() 时,根据两根大小再分类讨论对应单调区间, (2)先化简不等式
时,根据两根大小再分类讨论对应单调区间, (2)先化简不等式![]() 消m得
消m得![]() ,再利用导数研究
,再利用导数研究![]() ,
,![]() 单调性,得其最小值大于-1,即证得结果.
单调性,得其最小值大于-1,即证得结果.
详解:(1)由![]() ,得
,得
![]()
![]() ,
,![]() .
.
设![]() ,
,![]() .
.
当![]() 时,即
时,即![]() 时,
时,![]() ,
,![]() .
.
∴![]() 在
在![]() 上单调递减.
上单调递减.
当![]() 时,即
时,即![]() 时,
时,
令![]() ,得
,得![]() ,
,![]() ,
,![]() .
.
当![]() 时,
时,![]() ,
,
在![]() 上,
上,![]() ,在
,在![]() 上,
上,![]() ,
,
∴![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
综上,当![]() 时,
时,![]() 在
在![]() 上单调递减,
上单调递减,
当![]() 时,
时,![]() 在
在![]() ,
,![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(2)∵![]() 有两个极值点
有两个极值点![]() ,
,![]() ,且
,且![]() ,
,
∴由(1)知![]() 有两个不同的零点
有两个不同的零点![]() ,
,![]() ,
,
![]() ,
,![]() ,且
,且![]() ,此时,
,此时,![]() ,
,
要证明![]() ,只要证明
,只要证明![]() .
.
∵![]() ,∴只要证明
,∴只要证明![]() 成立.
成立.
∵![]() ,∴
,∴![]() .
.
设![]() ,
,![]() ,
,
则![]() ,
,
当![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() ,即
,即![]() ,
,
∴![]() 有两个极值点
有两个极值点![]() ,
,![]() ,且
,且![]() 时,
时,![]() .
.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】现有10道题,其中6道甲类题,4道乙类题,张同学从中任取3道题解答.
(I)求张同学至少取到1道乙类题的概率;
(II)已知所取的3道题中有2道甲类题,1道乙类题.设张同学答对甲类题的概率都是![]() ,答对每道乙类题的概率都是
,答对每道乙类题的概率都是![]() ,且各题答对与否相互独立.用
,且各题答对与否相互独立.用![]() 表示张同学答对题的个数,求
表示张同学答对题的个数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】当x∈R,|x|<1时,有如下表达式:1+x+x2+…+xn+…= ![]()
两边同时积分得: ![]() dx+
dx+ ![]() xdx+
xdx+ ![]() x2dx+…+
x2dx+…+ ![]() xndx+…=
xndx+…= ![]()
![]() dx
dx
从而得到如下等式:1× ![]() +
+ ![]() ×(
×( ![]() )2+
)2+ ![]() ×(
×( ![]() )3+…+
)3+…+ ![]() ×(
×( ![]() )n+1+…=ln2
)n+1+…=ln2
请根据以上材料所蕴含的数学思想方法,计算:![]() ×
× ![]() +
+ ![]()
![]() ×(
×( ![]() )2+
)2+ ![]()
![]() ×(
×( ![]() )3+…+
)3+…+ ![]()
![]() ×(
×( ![]() )n+1= .
)n+1= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次测试中,卷面满分为100分,考生得分为整数,规定60分及以上为及格.某调研课题小组为了调查午休对考生复习效果的影响,对午休和不午休的考生进行了测试成绩的统计,数据如下表:

(1)根据上述表格完成下列列联表:

(2)判断“能否在犯错误的概率不超过0.010的前提下认为成绩及格与午休有关”?
(参考公式:![]() ,其中
,其中![]() .)
.)
| 0.010 | 0.05 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某保险公司针对企业职工推出一款意外险产品,每年每人只要交少量保费,发生意外后可一次性获赔50万元.保险公司把职工从事的所有岗位共分为![]() 、
、![]() 、
、![]() 三类工种,根据历史数据统计出三类工种的每赔付频率如下表(并以此估计赔付概率).
三类工种,根据历史数据统计出三类工种的每赔付频率如下表(并以此估计赔付概率).


(Ⅰ)根据规定,该产品各工种保单的期望利润都不得超过保费的20%,试分别确定各类工种每张保单保费的上限;
(Ⅱ)某企业共有职工20000人,从事三类工种的人数分布比例如图,老板准备为全体职工每人购买一份此种保险,并以(Ⅰ)中计算的各类保险上限购买,试估计保险公司在这宗交易中的期望利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
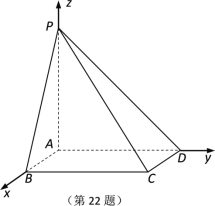
【题目】如图所示,在四棱锥![]() 中,底面
中,底面![]() 是矩形,
是矩形,![]() 平面
平面![]() ,AB 1,AP AD 2.
,AB 1,AP AD 2.
(1)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(2)若点M,N分别在AB,PC上,且![]() 平面
平面![]() ,试确定点M,N的位置.
,试确定点M,N的位置.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为保障高考的公平性,高考时每个考点都要安装手机屏蔽仪,要求在考点周围1 km内不能收到手机信号,检查员抽查某市一考点,在考点正西约![]() km/h的的B处有一条北偏东60°方向的公路,在此处检查员用手机接通电话,以每小时12千米的速度沿公路行驶,最多需要多少时间,检查员开始收不到信号,并至少持续多长时间该考点才算合格?
km/h的的B处有一条北偏东60°方向的公路,在此处检查员用手机接通电话,以每小时12千米的速度沿公路行驶,最多需要多少时间,检查员开始收不到信号,并至少持续多长时间该考点才算合格?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com