
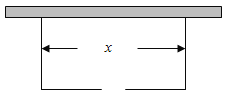
【题目】围建一个面积为360![]() 的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为
的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为![]() (单位:
(单位:![]() ),修建此矩形场地围墙的总费用为
),修建此矩形场地围墙的总费用为![]() (单位:元)
(单位:元)
(1)将![]() 表示为
表示为![]() 的函数;
的函数;
(2)试确定![]() ,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
【答案】(1)![]() ;(2)当x=24m时,修建围墙的总费用最小,最小总费用是10440元.
;(2)当x=24m时,修建围墙的总费用最小,最小总费用是10440元.
【解析】试题分析:(1)设矩形的另一边长为am,则根据围建的矩形场地的面积为360m2,易得![]() ,此时再根据旧墙的维修费用为45元/m,新墙的造价为180元/m,我们即可得到修建围墙的总费用y表示成x的函数的解析式;(2)根据(1)中所得函数的解析式,利用基本不等式,我们易求出修建此矩形场地围墙的总费用最小值,及相应的x值
,此时再根据旧墙的维修费用为45元/m,新墙的造价为180元/m,我们即可得到修建围墙的总费用y表示成x的函数的解析式;(2)根据(1)中所得函数的解析式,利用基本不等式,我们易求出修建此矩形场地围墙的总费用最小值,及相应的x值
试题解析:(1)如图,设矩形的另一边长为a m
则![]() 45x+180(x-2)+180·2a=225x+360a-360
45x+180(x-2)+180·2a=225x+360a-360
由已知xa=360,得a=![]() ,
,
所以y=225x+![]()
(2)![]()
![]() .当且仅当225x=
.当且仅当225x=![]() 时,等号成立.
时,等号成立.
即当x=24m时,修建围墙的总费用最小,最小总费用是10440元.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:
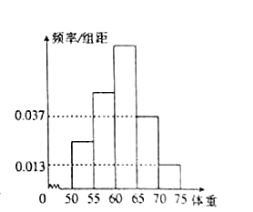
【题目】为了解今年某校高三毕业班想参军的学生体重情况,将所得的数据整理后,画出了频率分布直方图(如图).已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为24.
(Ⅰ)求该校高三毕业班想参军的学生人数;
(Ⅱ)以这所学校的样本数据来估计全省的总体数据,若从全省高三毕业班想参军的同学中(人数很多)任选三人,设![]() 表示体重超过60公斤的学生人数,求
表示体重超过60公斤的学生人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高2010级数学培优学习小组有男生3人女生2人,这5人站成一排留影。
(1)求其中的甲乙两人必须相邻的站法有多少种?
(2)求其中的甲乙两人不相邻的站法有多少种?
(3)求甲不站最左端且乙不站最右端的站法有多少种 ?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】迭代法是用于求方程或方程组近似根的一种常用的算法设计方法.设方程为![]() ,用某种数学方法到处等价的形式
,用某种数学方法到处等价的形式![]() ,然后按以下步骤执行:
,然后按以下步骤执行:
(1)选一个方程的近似根,赋给变量![]() ;
;
(2)将![]() 的值保存于变量
的值保存于变量![]() ,然后计算
,然后计算![]() ,并将结果存于变量
,并将结果存于变量![]() ;
;
(3)当![]() 与
与![]() 的差的绝对值还小于指定的精度要求时,重复步骤(2)的计算.若方程有根,则按上述方法求得的
的差的绝对值还小于指定的精度要求时,重复步骤(2)的计算.若方程有根,则按上述方法求得的![]() 就认为是方程的根.试用迭代法求某个数的平方根,用流程图和伪代码表示问题的算法.
就认为是方程的根.试用迭代法求某个数的平方根,用流程图和伪代码表示问题的算法.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种商品原来每件售价为25元,年销售8万件.
(1)据市场调查,若价格每提高1元,销售量将相应减少2000件,要使销售的总收入不低于原收入,该商品每件定价最多为多少元?
(2)为了扩大该商品的影响力,提高年销售量,公司决定明年对该商品进行全面技术革新和营销策略改革,并提高定价到![]() 元,公司拟投入
元,公司拟投入![]() 万元作为技改费用,投入50万元作为固定宣传费用,投入
万元作为技改费用,投入50万元作为固定宣传费用,投入![]() 作为浮动宣传费用.试问:当该商品明年的销售量
作为浮动宣传费用.试问:当该商品明年的销售量![]() 至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com