
���� ��1�����������ʼ�ͨ�����췽���飬���a��b��
��2��ֱ������Բ����������Τ�ﶨ�����ҳ���ʽ�������������֤��|PA|2+|PB|2Ϊ��ֵ��
��� �⣺��1��������ɵ÷�����$\left\{\begin{array}{l}{{e}^{2}=1-\frac{{b}^{2}}{{a}^{2}}}\\{\frac{2{b}^{2}}{a}=\frac{32}{5}}\end{array}\right.$
���$\left\{\begin{array}{l}{a=5}\\{b=4}\end{array}\right.$
����Բ������Ϊ$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{16}=1$������4�֣�
��2����l�ķ���Ϊ$x=\frac{5}{4}y+m$������$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{16}=1$
�������ã�25y2+20my+8��m2-25��=0����6�֣�
��A��x1��y1����B��x2��y2������${y}_{1}+{y}_{2}=-\frac{4}{5}m$��${y}_{1}{y}_{2}=\frac{8��{m}^{2}-25��}{25}$��
�֡�$|PA{|}^{2}=��{x}_{1}-m��^{2}+{{y}_{1}}^{2}$=$\frac{41}{16}{{y}_{1}}^{2}$��ͬ��$|PB{|}^{2}=\frac{41}{16}{{y}_{2}}^{2}$����8�֣�
��$|PA{|}^{2}+|PB{|}^{2}=\frac{41}{16}��{{y}_{1}}^{2}+{{y}_{2}}^{2}��$
=$\frac{41}{16}$$[��{y}_{1}+{y}_{2}��^{2}-2{y}_{1}{y}_{2}]$
=$\frac{41}{16}$$[��-\frac{4m}{5}��^{2}-\frac{16��{m}^{2}-25��}{25}]$
=41��
����|PA|2+|PB|2�Ƕ�ֵ����12�֣�
���� ��������Բ�����̣�ֱ������Բλ�ù�ϵ��Բ�����ж��㶨ֵ���⣮���������跽�̣�����˼�룬������������е��⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
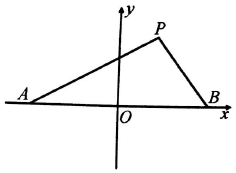 ��ͼ�����A��B������ֱ�Ϊ��-$\sqrt{3}$��0������$\sqrt{3}$��0����ֱ��AP��BP�ཻ�ڵ�P�������ǵ�б��֮��Ϊ-$\frac{2}{3}$��
��ͼ�����A��B������ֱ�Ϊ��-$\sqrt{3}$��0������$\sqrt{3}$��0����ֱ��AP��BP�ཻ�ڵ�P�������ǵ�б��֮��Ϊ-$\frac{2}{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
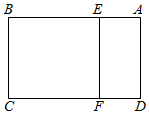 ��ͼ���ھ���ABCD�У�AD=$\sqrt{5}$��AB=3��E��F�ֱ�ΪAB�ߡ�CD����һ�㣬��AE=DF=l���ֽ�����ABCD��EF����ʹ��ƽ��ADFE��ƽ��BCFE������AB��CD��������������ABE-DCF�IJ������ԭ����ABCD�������Լ�ࣨȡ$\sqrt{5}$��2.236����������
��ͼ���ھ���ABCD�У�AD=$\sqrt{5}$��AB=3��E��F�ֱ�ΪAB�ߡ�CD����һ�㣬��AE=DF=l���ֽ�����ABCD��EF����ʹ��ƽ��ADFE��ƽ��BCFE������AB��CD��������������ABE-DCF�IJ������ԭ����ABCD�������Լ�ࣨȡ$\sqrt{5}$��2.236����������| A�� | 68% | B�� | 70% | C�� | 72% | D�� | 75% |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ij�����ͼ��ͼ��ʾ�������������n�ֱ�Ϊ3��1������ͼ�пհ��жϿ���Ӧ�������������Ϊ��������
ij�����ͼ��ͼ��ʾ�������������n�ֱ�Ϊ3��1������ͼ�пհ��жϿ���Ӧ�������������Ϊ��������| A�� | i��7�� | B�� | i��7�� | C�� | i��6�� | D�� | i��6�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 0 | C�� | -2 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com