
已知函数
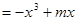 在
在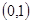 上是增函数,
上是增函数,
(1)求实数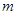 的取值集合
的取值集合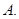 ;
;
(2)当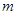 取值集合
取值集合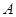 中的最小值时,定义数列
中的最小值时,定义数列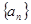 ;满足
;满足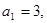 且
且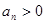 ,
,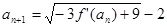 ,求数列
,求数列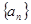 的通项公式;
的通项公式;
(3)若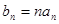 ,数列
,数列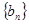 的前
的前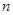 项和为
项和为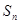 ,求证:
,求证: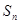
 .
.
(1)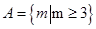 ;(2)
;(2) ;(3)详见解析
;(3)详见解析
解析试题分析:(1)函数 在区间
在区间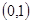 是增函数,说明
是增函数,说明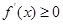 恒成立,再参变分离确定
恒成立,再参变分离确定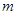 的取值集合
的取值集合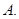 ;
;
(2)由(1)知 ,表示
,表示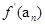 ,代入
,代入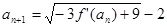 中,得关于
中,得关于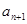 和
和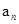 的递推式,再根据递推公式求通项公式,常见的根据递推公式求通项公式的方法有:①
的递推式,再根据递推公式求通项公式,常见的根据递推公式求通项公式的方法有:①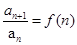 ,用累积法;②
,用累积法;② ,用累加法;③
,用累加法;③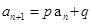 (p,q是常数),用构造法;④
(p,q是常数),用构造法;④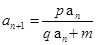 (p,q,m是常数),用两边取倒数,再用构造法,该题
(p,q,m是常数),用两边取倒数,再用构造法,该题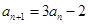 ,用③求
,用③求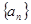 ;(3)首先求数列
;(3)首先求数列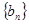 的通项公式,再根据通项公式的具体形式,选择合适的求和方法,常见的求和方法有①直接法,直接利用等比数列或等差数列前n项和公式;②裂项相消法,在求和的过程中互相抵消的办法;③错位相减法,适合于通项公式是等差数列乘以等比数列的类型;④分组求和法,分组分别求和再相加的办法;⑤奇偶并项求和法,研究奇数项和偶数项的特点来求和的办法,该题
的通项公式,再根据通项公式的具体形式,选择合适的求和方法,常见的求和方法有①直接法,直接利用等比数列或等差数列前n项和公式;②裂项相消法,在求和的过程中互相抵消的办法;③错位相减法,适合于通项公式是等差数列乘以等比数列的类型;④分组求和法,分组分别求和再相加的办法;⑤奇偶并项求和法,研究奇数项和偶数项的特点来求和的办法,该题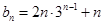 ,利用③④结合起来求和,再证明不等式成立.
,利用③④结合起来求和,再证明不等式成立.
试题解析:(1) 因为函数 在
在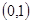 上是增函数,只需
上是增函数,只需 在
在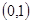 满足
满足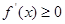 恒成立,即
恒成立,即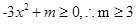 ,所以
,所以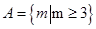 ;
;
(2)由(1)知 ,因为
,因为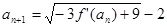 ,∴
,∴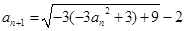 ,且
,且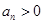 ,所以
,所以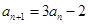 ,∴
,∴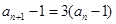 ,∴
,∴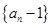 是以2为首项,3为公比的等比数列,故
是以2为首项,3为公比的等比数列,故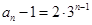 ,
, ;
;
(3)由(2)知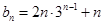 ,令
,令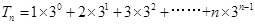 ,
,
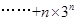 ,两式相减得
,两式相减得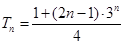 ,故
,故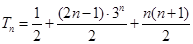
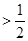 .
.
考点:1、导数在单调性上的应用;2、数列的递推公式;3、数列的前n项和.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
某出版社新出版一本高考复习用书,该书的成本为5元/本,经销过程中每本书需付给代理商m元(1≤m≤3)的劳务费,经出版社研究决定,新书投放市场后定价为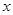 元/本(9≤
元/本(9≤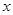 ≤11),预计一年的销售量为
≤11),预计一年的销售量为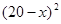 万本.
万本.
(1)求该出版社一年的利润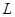 (万元)与每本书的定价
(万元)与每本书的定价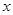 的函数关系式;
的函数关系式;
(2)当每本书的定价为多少元时,该出版社一年的利润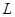 最大,并求出
最大,并求出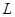 的最大值
的最大值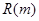 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数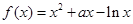 ,
, ;
;
(1)当 时,求函数
时,求函数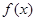 的单调区间;
的单调区间;
(2)若函数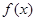 在[1,2]上是减函数,求实数
在[1,2]上是减函数,求实数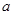 的取值范围;
的取值范围;
(3)令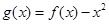 ,是否存在实数
,是否存在实数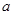 ,当
,当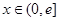 (
(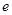 是自然对数的底数)时,函数
是自然对数的底数)时,函数 的最小值是
的最小值是 .若存在,求出
.若存在,求出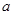 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=alnx+ (a≠0)在(0,
(a≠0)在(0, )内有极值.
)内有极值.
(I)求实数a的取值范围;
(II)若x1∈(0, ),x2∈(2,+∞)且a∈[
),x2∈(2,+∞)且a∈[ ,2]时,求证:f(x1)﹣f(x2)≥ln2+
,2]时,求证:f(x1)﹣f(x2)≥ln2+ .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数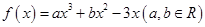 在点
在点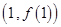 处的切线方程为
处的切线方程为 .
.
⑴求函数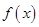 的解析式;
的解析式;
⑵若对于区间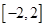 上任意两个自变量的值
上任意两个自变量的值 都有
都有 ,求实数
,求实数 的最小值;
的最小值;
⑶若过点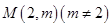 可作曲线
可作曲线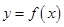 的三条切线,求实数
的三条切线,求实数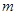 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知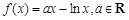 .
.
(1)当 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)若 在
在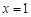 处有极值,求
处有极值,求 的单调递增区间;
的单调递增区间;
(3)是否存在实数 ,使
,使 在区间
在区间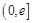 的最小值是3,若存在,求出
的最小值是3,若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com