
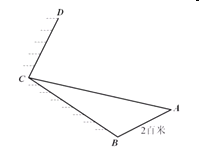
【题目】如图是一景区的截面图,![]() 是可以行走的斜坡,已知
是可以行走的斜坡,已知![]() 百米,
百米,![]() 是没有人行路(不能攀登)的斜坡,
是没有人行路(不能攀登)的斜坡,![]() 是斜坡上的一段陡峭的山崖.假设你(看做一点)在斜坡
是斜坡上的一段陡峭的山崖.假设你(看做一点)在斜坡![]() 上,身上只携带着量角器(可以测量以你为顶点的角).
上,身上只携带着量角器(可以测量以你为顶点的角).
(1)请你设计一个通过测量角可以计算出斜坡![]() 的长的方案,用字母表示所测量的角,计算出
的长的方案,用字母表示所测量的角,计算出![]() 的长,并化简;
的长,并化简;
(2)设![]() 百米,
百米,![]() 百米,
百米,![]() ,
,![]() ,求山崖
,求山崖![]() 的长.(精确到米)
的长.(精确到米)
【答案】(1)![]() 米,详见解析 (2)205米
米,详见解析 (2)205米
【解析】
(1)由题意测得![]() ,
,![]() ,在
,在![]() 中利用正弦定理求得
中利用正弦定理求得![]() 的值;
的值;
(2)解法一,![]() 中由余弦定理求得
中由余弦定理求得![]() ,
,![]() 中求得
中求得![]() 和
和![]() 的值,在
的值,在![]() 中利用余弦定理求得
中利用余弦定理求得![]() 的值.
的值.
解法二,![]() 中求得
中求得![]() ,
,![]() 中利用余弦定理求得
中利用余弦定理求得![]() ,利用三角恒等变换求得
,利用三角恒等变换求得![]() ,在
,在![]() 中利用余弦定理求得
中利用余弦定理求得![]() 的值.
的值.
解:(1)据题意,可测得![]() ,
,![]() ,
,
在![]() 中,由正弦定理,有
中,由正弦定理,有![]() ,
,
即![]() .
.
解得![]() (米).
(米).
(2)解一:在![]() 中,
中,![]() 百米,
百米,
![]() 百米,
百米,![]() 百米,
百米,
由余弦定理,可得![]() ,
,
解得![]() ,
,
∴![]() .
.
又由已知,在![]() 中,
中,![]() ,
,
可解得![]() ,从而的
,从而的![]() .
.
∵![]() ,
,
在![]() 中,由余弦定理得
中,由余弦定理得![]() 米
米
所以,![]() 的长度约为205米.
的长度约为205米.

解二:(2)在![]() 中,求得
中,求得![]() .
.
在![]() 中,由余弦定理,得
中,由余弦定理,得![]() ,
,
进而得![]() ,再由
,再由![]() 可求得
可求得![]() ,
,![]()
![]() .
.
在![]() 中,由余弦定理,得
中,由余弦定理,得![]() .
.
所以,![]() 的长度约为205米.
的长度约为205米.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设F1,F2分别是椭圆E: ![]() (a>b>0)的左、右焦点,过点F1的直线交椭圆E于A,B两点,|AF1|=3|BF1|,若cos∠AF2B=
(a>b>0)的左、右焦点,过点F1的直线交椭圆E于A,B两点,|AF1|=3|BF1|,若cos∠AF2B=![]() ,则椭圆E的离心率为( )
,则椭圆E的离心率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一元二次函数![]() 的图像与
的图像与![]() 轴有两个不同的交点,其中一个交点的坐标为
轴有两个不同的交点,其中一个交点的坐标为![]() 且当
且当![]() 时,恒有
时,恒有![]()
(1)求出不等式![]() 的解(用
的解(用![]() 表示);
表示);
(2)若以二次函数的图像与坐标轴的三个交点为顶点的三角形的面积为8,求![]() 的取值范围;
的取值范围;
(3)若不等式![]() 对所有
对所有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 为偶函数,函数
为偶函数,函数![]() 为奇函数。
为奇函数。![]() 对任意实数x恒成立.
对任意实数x恒成立.
(1)求函数![]() 与
与![]() ;
;
(2)设![]() ,
,![]() ,若
,若![]() 对于
对于![]() 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;
(3)对于(2)中的函数![]() ,若方程
,若方程![]() 没有实数解,实数m的取值范围.
没有实数解,实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,圆C的参数方程为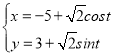 ,(t为参数),在以原点O为极点,x轴的非负半轴为极轴建立的极坐标系中,直线l的极坐标方程为
,(t为参数),在以原点O为极点,x轴的非负半轴为极轴建立的极坐标系中,直线l的极坐标方程为![]() ,A,B两点的极坐标分别为
,A,B两点的极坐标分别为![]() .
.
(1)求圆C的普通方程和直线l的直角坐标方程;
(2)点P是圆C上任一点,求△PAB面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在R上的奇函数,当
是定义在R上的奇函数,当![]() 时,
时,![]() .
.
(Ⅰ)求函数![]() 在R上的解析式;
在R上的解析式;
(Ⅱ)若![]() ,函数
,函数![]() ,是否存在实数m使得
,是否存在实数m使得![]() 的最小值为
的最小值为![]() ,若存在,求m的值;若不存在,请说明理由.
,若存在,求m的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校计划利用周五下午第一、二、三节课举办语文、数学、英语、理综4科的专题讲座,每科一节课,每节至少有一科,且数学、理综不安排在同一节,则不同的安排方法共有( )
A. 6种 B. 24种 C. 30种 D. 36种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com