
【题目】如图,在三棱柱![]() 中,点P,G分别是
中,点P,G分别是![]() ,
,![]() 的中点,已知
的中点,已知![]() ⊥平面ABC,
⊥平面ABC,![]() =
=![]() =3,
=3,![]() =
=![]() =2.
=2.
(I)求异面直线![]() 与AB所成角的余弦值;
与AB所成角的余弦值;
(II)求证:![]() ⊥平面
⊥平面![]() ;
;
(III)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.

【答案】(Ⅰ)![]() (Ⅱ)见解析(Ⅲ)
(Ⅱ)见解析(Ⅲ)![]()
【解析】分析:(Ⅰ)由题意得![]() ∥AB,故∠G
∥AB,故∠G![]() 是异面直线
是异面直线![]() 与AB所成的角,解三角形可得所求余弦值.(Ⅱ)在三棱柱
与AB所成的角,解三角形可得所求余弦值.(Ⅱ)在三棱柱![]() 中,由
中,由![]() ⊥平面ABC可得
⊥平面ABC可得![]() ⊥A1G,于是
⊥A1G,于是![]() ⊥A1G,又A1G⊥
⊥A1G,又A1G⊥![]() ,根据线面垂直的判定定理可得结论成立.(Ⅲ)取
,根据线面垂直的判定定理可得结论成立.(Ⅲ)取![]() 的中点H,连接AH,HG;取HG的中点O,连接OP,
的中点H,连接AH,HG;取HG的中点O,连接OP,![]() .由PO//A1G可得
.由PO//A1G可得![]() 平面
平面![]() ,
,
故得∠PC1O是PC1与平面![]() 所成的角,然后解三角形可得所求.
所成的角,然后解三角形可得所求.
详解:

(I)∵![]() ∥AB,
∥AB,
∴∠G![]() 是异面直线
是异面直线![]() 与AB所成的角.
与AB所成的角.
∵![]() =
=![]() =2,G为BC的中点,
=2,G为BC的中点,
∴A1G⊥B1C1,
在![]() 中,
中,![]() ,
,
∴ ,
,
即异面直线AG与AB所成角的余炫值为![]() .
.
(II)在三棱柱![]() 中,
中,
∵![]() ⊥平面ABC,
⊥平面ABC,![]() 平面ABC,
平面ABC,
∴![]() ⊥A1G,
⊥A1G,
∴![]() ⊥A1G,
⊥A1G,
又A1G⊥![]() ,
,![]() ,
,
∴![]() 平面
平面![]() .
.
(III)解:取![]() 的中点H,连接AH,HG;取HG的中点O,连接OP,
的中点H,连接AH,HG;取HG的中点O,连接OP,![]() .
.
∵PO//A1G,
∴![]() 平面
平面![]() ,
,
∴∠PC1O是PC1与平面![]() 所成的角.
所成的角.
由已知得,![]() ,
,
∴![]()
∴直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】数学家欧拉在1765年发现,任意三角形的外心、重心、垂心位于同一条直线上,这条直线称为欧拉线已知![]() 的顶点
的顶点![]() ,若其欧拉线的方程为
,若其欧拉线的方程为![]() ,则顶点
,则顶点![]() 的坐标为( )
的坐标为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 已知2Sn=3n+1+2n﹣3.
(1)求数列{an}的通项公式;
(2)求数列{nan}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|ω|< ![]() )的部分图象如图所示,下列说法正确的是( )
)的部分图象如图所示,下列说法正确的是( ) 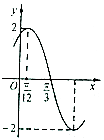
A.函数f(x)的最小正周期为2π
B.函数f(x)的图象关于点(﹣ ![]() ,0)对称
,0)对称
C.将函数f(x)的图象向左平移 ![]() 个单位得到的函数图象关于y轴对称
个单位得到的函数图象关于y轴对称
D.函数f(x)的单调递增区间是[kπ+ ![]() ,kπ+
,kπ+ ![]() ](K∈Z)
](K∈Z)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若直线ax+by—4=0和圆x2+y2=4没有公共点,则过点(a,b)的直线与椭圆![]() +
+![]() =1的公共点个数为( )
=1的公共点个数为( )
A. 0 B. 1 C. 2 D. 由a,b的取值来确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一动圆与定圆![]() 外切,同时和圆
外切,同时和圆![]() 内切,定点A(1,1).
内切,定点A(1,1).
(1)求动圆圆心P的轨迹E的方程,并说明是何种曲线;
(2)M为E上任意一点, F为E的左焦点,试求![]() 的最小值;
的最小值;
(3)试求![]() 的取值范围;
的取值范围;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF ![]() 2CE,G是线段BF上一点,AB=AF=BC=2.
2CE,G是线段BF上一点,AB=AF=BC=2. 
(1)当GB=GF时,求证:EG∥平面ABC;
(2)求二面角E﹣BF﹣A的余弦值;
(3)是否存在点G满足BF⊥平面AEG?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com