
���� ��1��ͨ������P������Բ���̲�����������Ϊ$\frac{\sqrt{2}}{2}$�����㼴�ý��ۣ�
��2���ȼ������һ������P��ʹ����ABΪֱ����Բ������㣬���ô�ֱʱ��$\overrightarrow{PA}•\overrightarrow{PB}$=0���õ�����ֱ��б��k�ķ��̣���k���������������ڣ����������ڣ�
��� �⣺��1����������Ϊ$\frac{\sqrt{2}}{2}$���ҹ�����M��1��$\frac{\sqrt{2}}{2}$������$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$��$\frac{1}{{a}^{2}}+\frac{\frac{1}{2}}{{b}^{2}}$=1����ã�a=$\sqrt{2}$��b=1��
������ԲC�ķ�����$\frac{{x}^{2}}{2}+{y}^{2}$=1��
��2����ֱ��l��x��ƽ��ʱ����ABΪֱ����Բ����Ϊ${x}^{2}+��y+\frac{1}{3}��^{2}=��\frac{4}{3}��^{2}$
��ֱ��l��y���غ�ʱ����ABΪֱ����Բ����Ϊx2+y2=1
������Բ���е�Ϊ�㣨0��1��
����ĵ�PΪ�㣨0��1����֤�����£�
ֱ��l��y=kx-$\frac{1}{3}$��k��R������Բ���������ã�18k2+9��x2-12kx-16=0
��A��x1��y1����B��x2��y2����x1+x2=$\frac{12k}{18{k}^{2}+9}$��x1x2=-$\frac{16}{18{k}^{2}+9}$��
$\overrightarrow{PA}•\overrightarrow{PB}$=��1+k2��x1x2-$\frac{4}{3}$k��x1+x2��+$\frac{16}{9}$
=��1+k2��•��-$\frac{16}{18{k}^{2}+9}$��-$\frac{4}{3}$k•$\frac{12k}{18{k}^{2}+9}$+$\frac{16}{9}$=0��
����$\overrightarrow{PA}��\overrightarrow{PB}$������ABΪֱ����Բ���㣨0��1��
���Դ���һ������P��ʹ����ABΪֱ����Բ�������P��0��1����
���� ���⿼������Բ����Բ��ֱ�ߵ��ۺ����ã����⣬�����������֪ʶ���ۺ���ǿ�������������


 Сѧѧϰ�ð���ϵ�д�
Сѧѧϰ�ð���ϵ�д� Сѧͬ�����������ܾ�ϵ�д�
Сѧͬ�����������ܾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
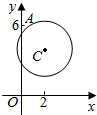 ��֪ij��Ұ�����������ͻ���û����λ����Ϊ����·������������A���������y�Ḻ������ֱ�ߣ�������ð�մ�ԽҰ����������ͼ�����ϻ���û������ΪԲC����x-2��2+��y-4��2=$\frac{25}{4}$����������λ�����A��0��6����O��Ҫ40min������λ�������ϻ���û�ĵ�������ʱ�䳬��15min��������Σ�գ��ʣ���λ�����Ƿ�������Σ�գ���������λ���������ٷ���������
��֪ij��Ұ�����������ͻ���û����λ����Ϊ����·������������A���������y�Ḻ������ֱ�ߣ�������ð�մ�ԽҰ����������ͼ�����ϻ���û������ΪԲC����x-2��2+��y-4��2=$\frac{25}{4}$����������λ�����A��0��6����O��Ҫ40min������λ�������ϻ���û�ĵ�������ʱ�䳬��15min��������Σ�գ��ʣ���λ�����Ƿ�������Σ�գ���������λ���������ٷ����������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2��10 | B�� | 10 | C�� | 2 | D�� | 4��8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
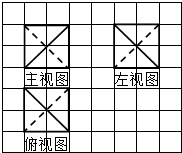
| A�� | $\frac{2\sqrt{3}}{9��}$ | B�� | $\frac{\sqrt{3}}{9��}$ | C�� | $\frac{\sqrt{2}}{16��}$ | D�� | $\frac{8\sqrt{2}}{��}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com