②③
分析:对于①,分别举反例说明充分性和必要性都不成立:函数y=|x|,在x=0处取极小值但f′(0)≠0,说明充分性不成立;函数f(x)=x
3在x=0处,f′(x)=0,而f(0)并非函数的极值,必要性质不成立.由此进行判断.
对于②,分析题意,2和3相邻的偶数有两类,一类是2在末位,两数相邻不交换,一类是4在末位,两数相邻可交换,分类计数,再求两者的和得到答案;
对于③,由函数是偶函数及θ的范围求出θ的值,再由|x
2-x
1|的最小值为π得到w的值.从而得到函数的解析式.
对于④,由双曲线的定义知||PF
1|-|PF
2||=2a,结合其几何特征,计算可得答案.
解答:对于①,先说明充分性不成立,
例如函数y=|x|,在x=0处取得极小值f(0)=0,但f′(x)在x=0处无定义,
说明f′(0)=0不成立,因此充分性不成立;
再说明必要性不成立,设函数f(x)=x
3,则f′(x)=3x
2
在x=0处,f′(x)=0,但x=0不是函数f(x)的极值点,故必要性质不成立.故①错;
对于②,由题意,
若2在末位,则需要从余下的三个数中选出三个数排在百位、千位与万位,故不同的排法有A
33=6种
若2不在末位,则必有4在末位,由此,2,3二数先捆在一起,再与两奇数一起参加排列,总的排法有A
22×A
33=12,
综上由数字1,2,3,4,5所组成的没有重复数字的五位数中,2和3相邻的偶数共有6+12=18个.故②正确;
对于③:∵y=2sin(wx+θ)为偶函数∴θ=

+kπ k∈z 又∵0<θ<π∴θ=

由诱导公式得函数y=2coswx 又∵其图象与直线y=2某两个交点的横坐标分别为x
1,x
2,若|x
2-x
1|的最小值为π
∴函数的周期为π 即 w=2.故③正确;
对于④:∵双曲线的a=1,b=3,c=

,
由双曲线的定义知||PF
1|-|PF
2||=2a=2,
∴|PF
1|-4=±2,
∴|PF
1|=6或2,但是|PF
1|≥c-a=

-1,故|PF
1|=2舍去.故④错.
故答案为:②③.
点评:本题考查双曲线的简单性质、命题的真假判断与应用、函数在某点取得极值的条件、排列、组合及简单计数问题、正弦函数的奇偶性竺,解题时要认真审题,仔细解答.

 .
. =1上一点,F1、F2分别为双曲线的左右焦点,且|PF2|=4,则|PF1|=2或6.
=1上一点,F1、F2分别为双曲线的左右焦点,且|PF2|=4,则|PF1|=2或6. +kπ k∈z 又∵0<θ<π∴θ=
+kπ k∈z 又∵0<θ<π∴θ=
 ,
, -1,故|PF1|=2舍去.故④错.
-1,故|PF1|=2舍去.故④错.

 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案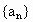 成等比数列,
成等比数列,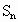 是前n项和,则
是前n项和,则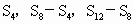 成等比数列;
成等比数列;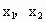 ,若
,若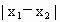 的最小值为π,则ω的值为2,θ的值为
的最小值为π,则ω的值为2,θ的值为 ;
;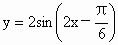 的图象的一个对称点是
的图象的一个对称点是 .
.