
【题目】已知椭圆![]() (
(![]() )的焦距为2,椭圆
)的焦距为2,椭圆![]() 的左右焦点分别为
的左右焦点分别为![]()
![]() ,过右焦点
,过右焦点![]() 作
作![]() 轴的垂线交椭圆于
轴的垂线交椭圆于![]()
![]() 两点,
两点,![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过右焦点![]() 作直线交椭圆于
作直线交椭圆于![]()
![]() 两点,若△
两点,若△![]() 的内切圆的面积为
的内切圆的面积为![]() ,求△
,求△![]() 的面积;
的面积;
(3)已知![]() ,
,![]() 为圆上一点(
为圆上一点(![]() 在
在![]() 轴右侧),过
轴右侧),过![]() 作圆的切线交椭圆
作圆的切线交椭圆![]() 于
于![]()
![]() 两点,试问△
两点,试问△![]() 的周长是否为一定值?若是,求出该定值,若不是,请说明理由.
的周长是否为一定值?若是,求出该定值,若不是,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)是,
;(3)是,![]() .
.
【解析】
(1)由题意结合椭圆的性质可得![]() ,再由点
,再由点![]() 即可求得
即可求得![]() 、
、![]() ,即可得解;
,即可得解;
(2)由题意结合椭圆的性质可得△![]() 的周长
的周长![]() ,再由
,再由![]() (
(![]() 为内切圆半径)即可得解;
为内切圆半径)即可得解;
(3)按照![]() 斜率是否存在讨论,当直线
斜率是否存在讨论,当直线![]() 斜率存在时,设
斜率存在时,设![]() ,
,![]() ,由两点之间距离公式、椭圆性质可得焦半径
,由两点之间距离公式、椭圆性质可得焦半径![]() 、
、![]() ,联立方程结合韦达定理、弦长公式可得
,联立方程结合韦达定理、弦长公式可得![]() ,再由直线
,再由直线![]() 与圆相切可得
与圆相切可得![]() ,代入运算即可得解.
,代入运算即可得解.
(1)由椭圆焦距为2可得![]() ,
,![]() ,
,
又过右焦点![]() 作
作![]() 轴的垂线交椭圆于
轴的垂线交椭圆于![]() 、
、![]() 两点,
两点,![]() ,
,
不妨设点![]() ,则
,则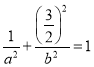 ,解得
,解得![]() ,
,![]() ,
,
所以椭圆![]() 的方程为
的方程为![]() ;
;
(2)由题意△![]() 的周长
的周长![]() ,
,
又△![]() 的内切圆的面积为
的内切圆的面积为![]() ,所以△
,所以△![]() 的内切圆的半径为
的内切圆的半径为![]() ,
,
所以△![]() 的面积
的面积![]() ;
;
(3)由题意![]() ,圆心为
,圆心为![]() ,半径为
,半径为![]() ,
,
若![]() 斜率不存在时,不妨设点
斜率不存在时,不妨设点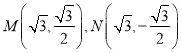 ,
,
此时△![]() 的周长
的周长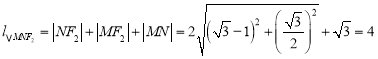 ;
;
当直线![]() 斜率存在时,设
斜率存在时,设![]() ,
,![]() ,
,
则![]() 即
即![]() ,
,
则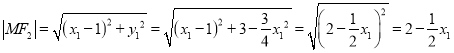 ,
,
同理,![]() ,
,
由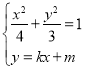 消去y得
消去y得![]() ,
,![]() ,
,
则![]() ,
,
由直线![]() 与
与![]() 相切可得
相切可得![]() ,即
,即![]() ,
,
所以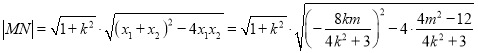
![]() ,
,
因为![]() 在
在![]() 轴右侧,所以
轴右侧,所以![]() ,
,
所以![]()
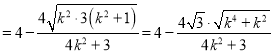 ,
,
所以△![]() 的周长
的周长![]()
![]() ;
;
综上,△![]() 的周长为一定值,且周长
的周长为一定值,且周长![]() .
.


科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 过点
过点![]() ,其参数方程为
,其参数方程为 (
(![]() 为参数,
为参数,![]() ),以
),以![]() 为极点,
为极点,![]() 轴非负半轴为极轴建立极坐标系,曲线
轴非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)求已知曲线![]() 和曲线
和曲线![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地有三家工厂,分别位于矩形ABCD的顶点A,B,及CD的中点P处,已知![]() km,
km,![]() ,为了处理三家工厂的污水,现要在矩形ABCD的区域上(含边界),且A,B与等距离的一点O处建造一个污水处理厂,并铺设排污管道AO,BO,OP,设排污管道的总长为ykm.
,为了处理三家工厂的污水,现要在矩形ABCD的区域上(含边界),且A,B与等距离的一点O处建造一个污水处理厂,并铺设排污管道AO,BO,OP,设排污管道的总长为ykm.
(I)按下列要求写出函数关系式:
①设![]() ,将
,将![]() 表示成
表示成![]() 的函数关系式;
的函数关系式;
②设![]() ,将
,将![]() 表示成
表示成![]() 的函数关系式.
的函数关系式.
(Ⅱ)请你选用(I)中的一个函数关系式,确定污水处理厂的位置,使三条排水管道总长度最短.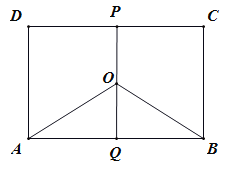
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有4位同学在同一天的上午、下午参加“身高与体重”、“立定跳远”、“肺活量”、“握力”、“台阶”五个项目的测试,每位同学测试两个项目,分别在上午和下午,且每人上午和下午测试的项目不能相同.若上午不测“握力”,下午不测“台阶”,其余项目上午、下午都各测试一人,则不同的安排方式的种数为( )
A.264B.72C.266D.274
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国人民大学发布的《中国大学生创业报告》显示,在国家“双创”政策的引导下,随着社会各方对于大学生创业实践的支持力度不断加强,大学生创业意向高涨,近九成的在校大学生曾考虑过创业,近两成的学生有强烈的创业意向. 数据充分表明,大学生正以饱满的热情投身到创新创业的大潮之中,大学生创业实践正呈现出生机勃勃的态势。小张大学毕业后从2008年年初开始创业,下表是2019年春节他将自己从2008—2018年的净利润按年度给出的一个总的统计表(为方便运算,数据作了适当的处理,单位:万元).
年度 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
利润 | 6 | 7 | 8 | 9 | 10 | 10 | 11 | 12 | 13 | 13 | 14 |
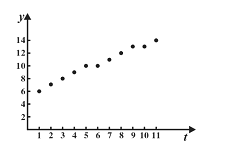
(Ⅰ)散点图如图所示,根据散点图指出年利润![]() (单位:万元)和年份序号
(单位:万元)和年份序号![]() 之间是否具有线性关系?并用相关系数说明用线性回归模型描述年净利润
之间是否具有线性关系?并用相关系数说明用线性回归模型描述年净利润![]() 与年份序号
与年份序号![]() 之间关系的效果;
之间关系的效果;
(Ⅱ)试用线性回归模型描述年净利润![]() 与年份序号
与年份序号![]() 之间的关系:求出年净利润
之间的关系:求出年净利润![]() 关于年份序号
关于年份序号![]() 的回归方程(系数精确到0.1),并帮小张估计他2019年可能赚到的净利润.
的回归方程(系数精确到0.1),并帮小张估计他2019年可能赚到的净利润.
附注:参考数据![]() .
.
参考公式: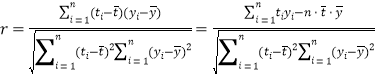 .
.![]() 且
且![]() 越大拟合效果越好.回归方程
越大拟合效果越好.回归方程![]() 斜率的最小二乘法估计公式为:
斜率的最小二乘法估计公式为: .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com