【题目】设
满足约束条件
且
的最小值为7，则
＝_________.
【答案】3
【解析】
根据约束条件画出可行域，再把目标函数转化为
，对参数a分类讨论，当
时显然不满足题意；当
时，直线经过可行域中的点A时，截距最小，即z有最小值，再由最小值为7，得出结果；当
时，的截距没有最小值，即z没有最小值；当
时，的截距没有最大值，即z没有最小值，综上可得出结果.
根据约束条件画出可行域如下：由
，可得出交点
，
由
可得，当时显然不满足题意；
当即
时，由可行域可知当直线经过可行域中的点A时，截距最小，即z有最小值，即
，解得
或
（舍）；
当即
时，由可行域可知的截距没有最小值，即z没有最小值；
当即
时，根据可行域可知的截距没有最大值，即z没有最小值.
综上可知满足条件时.
故答案为：3.
芝麻开花课程新体验系列答案科目：高中数学 来源： 题型：
【题目】已知椭圆
的长轴长为4，过点
且斜率为
的直线交椭圆于
两点，且点
为线段
的中点
（1）求椭圆
的方程；
（2）设点
为坐标原点，过右焦点
的直线交椭圆于
两点，（不在
轴上），求
面积
的最大值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
的图象与
轴的交点至少有一个在原点右侧．
（1）求实数
的取值范围；
（2）令
，求
的值（其中
表示不超过
的最大整数，例如：
，
)；
（3）对（2）中的求函数
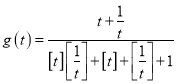的值域．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】近期，某公交公司分别推出支付宝和微信扫码支付乘车活动，活动设置了一段时间的推广期，由于推广期内优惠力度较大，吸引越来越多的人开始使用扫码支付，某线路公交车队统计了活动刚推出一周内每一天使用扫码支付的人次，用x表示活动推出的天数，y表示每天使用扫码支付的人次（单位：十人次），绘制了如图所示的散点图：
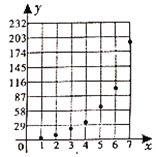
（I）根据散点图判断在推广期内，
与
（c，d为为大于零的常数）哪一个适宜作为扫码支付的人次y关于活动推出天数x的回归方程类型？（给出判断即可，不必说明理由）
（Ⅱ）根据（I）的判断结果求y关于x的回归方程，并预测活动推出第8天使用扫码支付的人次.
参考数据：
|
|
|
|
|
|
|
4 | 62 | 1.54 | 2535 | 50.12 | 140 | 3.47 |
其中
，
附：对于一组数据
，
，…，
，其回归直线
的斜率和截距的最小二乘估计分别为：
，
。
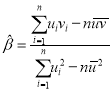查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】空气质量AQI指数是反映空气质量状况指数，AQI指数值越小，表明空气质量越好，其对应关系如表：
AQI指数值 |
|
|
|
|
|
|
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
如图所示的是某市11月1日至20日AQI指数变化的折线图：
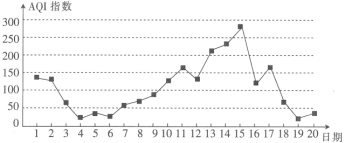
下列说法不正确的是（ ）
A.这
天中空气质量为轻度污染的天数占
B.这天中空气质量为优和良的天数为
天
C.这天中AQI指数值的中位数略低于
D.总体来说，该市11月上旬的空气质量比中旬的空气质量好
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】选修4-4：坐标系与参数方程
在直角坐标系
中，曲线
的参数方程为
（
为参数），以坐标原点为极点，
轴正半轴为极轴建立极坐标系，直线
的极坐标方程为
.
（1）求直线与曲线公共点的极坐标；
（2）设过点
的直线
交曲线于
，
两点，且
的中点为
，求直线的斜率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系
中，直线
的倾斜角为
，且经过点
，以坐标原点O为极点，
轴正半轴为极轴建立极坐标系，直线
，从原点O作射线交
于点M，点N为射线OM上的点，满足| 
，记点N的轨迹为曲线C．
（1）①设动点
，记
是直线的向上方向的单位方向向量，且
，以t为参数求直线的参数方程
②求曲线C的极坐标方程并化为直角坐标方程；
（2）设直线与曲线C交于P，Q两点，求
的值
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知两直线方程
与
，点
在
上运动，点
在
上运动，且线段
的长为定值
.
（Ⅰ）求线段的中点
的轨迹方程；
（Ⅱ）设直线
与点的轨迹相交于
，
两点，
为坐标原点，若
，求原点的直线
的距离的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
