
【题目】已知函数![]() .
.
(1)若![]() 在
在![]() 处取得极值,求
处取得极值,求![]() 的值;
的值;
(2)求![]() 在区间
在区间![]() 上的最小值;
上的最小值;
(3)在(1)的条件下,若![]() ,求证:当
,求证:当![]() 时,恒有
时,恒有![]() 成立.
成立.
【答案】(1)2;(2)![]() ;(3)证明见解析
;(3)证明见解析
【解析】
(1)先求出函数的定义域和导数,由已知函数![]() 在
在![]() 处取得极值,得到
处取得极值,得到![]() ,即可求解
,即可求解![]() 的值;
的值;
(2)由(1)得![]() ,定义域为
,定义域为![]() ,分
,分![]() ,
,![]() 和
和![]() 三种情况讨论,分别求得函数的最小值,即可得到结论;
三种情况讨论,分别求得函数的最小值,即可得到结论;
(3)由![]() ,得到
,得到![]() ,把
,把![]() ,只需证
,只需证![]() ,构造新函数
,构造新函数![]() ,利用导数求得函数的单调性与最值,即可求解.
,利用导数求得函数的单调性与最值,即可求解.
(1)由![]() ,定义域为
,定义域为![]() ,则
,则![]() ,
,
因为函数![]() 在
在![]() 处取得极值,
处取得极值,
所以![]() ,即
,即![]() ,解得
,解得![]() ,
,
经检验,满足题意,所以![]() .
.
(2)由(1)得![]() ,定义域为
,定义域为![]() ,
,
当![]() 时,有
时,有![]() ,
,![]() 在区间
在区间![]() 上单调递增,最小值为
上单调递增,最小值为![]() ,
,
当![]() 时,由
时,由![]() 得
得![]() ,且
,且![]() ,
,
当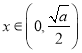 时,
时,![]() ,
,![]() 单调递减;
单调递减;
当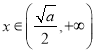 时,
时,![]() ,
,![]() 单调递增;
单调递增;
所以![]() 在区间
在区间![]() 上单调递增,最小值为
上单调递增,最小值为![]() ,
,
当![]() 时,则
时,则![]() ,当
,当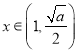 时,
时,![]() ,
,![]() 单调递减;
单调递减;
当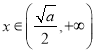 时,
时,![]() ,
,![]() 单调递增;
单调递增;
所以![]() 在
在![]() 处取得最小值
处取得最小值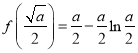 ,
,
综上可得:
当![]() 时,
时,![]() 在区间
在区间![]() 上的最小值为1,
上的最小值为1,
当![]() 时,
时,![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() .
.
(3)由![]() 得
得![]() ,
,
当![]() 时,
时,![]() ,则
,则![]() ,
,
欲证![]() ,只需证
,只需证![]() ,即证
,即证![]() ,即
,即![]() ,
,
设![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在区间
在区间![]() 上单调递增,
上单调递增,
![]() 当
当![]() 时,
时,![]() ,即
,即![]() ,
,
故![]() , 即当
, 即当![]() 时,恒有
时,恒有![]() 成立.
成立.


 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:高中数学 来源: 题型:
【题目】程大位是明代著名数学家,他的《新编直指算法统宗》是中国历史上一部影响巨大的著作.卷八中第33问:“今有三角果一垛,底阔每面七个.问该若干?”如图是解决该问题的程序框图.执行该程序框图,求得该垛果子的总数S为( )
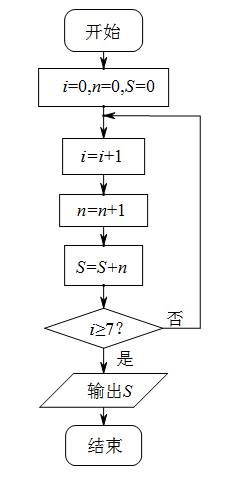
A.28B.56C.84D.120
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,下列给出四个结论:
,下列给出四个结论:
①![]() 的最大值为2;
的最大值为2;
②![]() 在区间
在区间![]() 上的单调增区间是
上的单调增区间是![]() ;
;
③在![]() 中,若
中,若![]() ,则
,则![]() ;
;
④将曲线![]() 向左平移
向左平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象,再将曲线
的图象,再将曲线![]()
所有点的纵坐标变为原来的2倍(横坐标不变),得到函数![]() 的导数
的导数![]() 的图象.其中正确的是_______________(填写所有正确结论的编号).
的图象.其中正确的是_______________(填写所有正确结论的编号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某客户准备在家中安装一套净水系统,该系统为二级过滤,使用寿命为十年如图所示两个二级过滤器采用并联安装,再与一级过滤器串联安装.
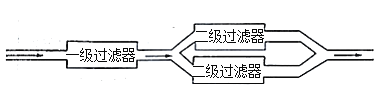
其中每一级过滤都由核心部件滤芯来实现在使用过程中,一级滤芯和二级滤芯都需要不定期更换(每个滤芯是否需要更换相互独立).若客户在安装净水系统的同时购买滤芯,则一级滤芯每个160元,二级滤芯每个80元.若客户在使用过程中单独购买滤芯则一级滤芯每个400元,二级滤芯每个200元.现需决策安装净水系统的同时购买滤芯的数量,为此参考了根据100套该款净水系统在十年使用期内更换滤芯的相关数据制成的图表,其中表1是根据100个一级过滤器更换的滤芯个数制成的频数分布表,图2是根据200个二级过滤器更换的滤芯个数制成的条形图.
表1:一级滤芯更换频数分布表
一级滤芯更换的个数 | 8 | 9 |
频数 | 60 | 40 |
图2:二级滤芯更换频数条形图
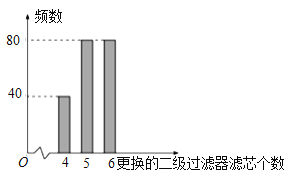
以100个一级过滤器更换滤芯的频率代替1个一级过滤器更换滤芯发生的概率,以200个二级过滤器更换滤芯的频率代替1个二级过滤器更换滤芯发生的概率.
(1)求一套净水系统在使用期内需要更换的各级滤芯总个数恰好为16的概率;
(2)记![]() 表示该客户的净水系统在使用期内需要更换的二级滤芯总数,求
表示该客户的净水系统在使用期内需要更换的二级滤芯总数,求![]() 的分布列及数学期望;
的分布列及数学期望;
(3)记![]() 分别表示该客户在安装净水系统的同时购买的一级滤芯和二级滤芯的个数.若
分别表示该客户在安装净水系统的同时购买的一级滤芯和二级滤芯的个数.若![]() ,且
,且![]() ,以该客户的净水系统在使用期内购买各级滤芯所需总费用的期望值为决策依据,试确定
,以该客户的净水系统在使用期内购买各级滤芯所需总费用的期望值为决策依据,试确定![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com