
| 1 | 20 |
 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源: 题型:
| 1 | 200 |
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:022
某工厂生产某种产品固定成本为2000万元,并且每生产一单位产品,成本增加10万元.又知总收入K是单位产品数Q的函数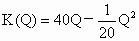 ,则总利润L(Q)的最大值是_____.
,则总利润L(Q)的最大值是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 Q2,则总利润L(Q)的最大值是________.
Q2,则总利润L(Q)的最大值是________.查看答案和解析>>
科目:高中数学 来源:2012-2013学年贵州省黔西南州兴义四中高三(上)9月月考数学试卷(文科)(解析版) 题型:填空题
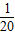 Q2,则总利润L(Q)的最大值是 .
Q2,则总利润L(Q)的最大值是 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com