
| 1 |
| 2 |
| 1 |
| 4 |
 解:由图知A(1,1),B(1,0),kOP=
解:由图知A(1,1),B(1,0),kOP=| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 2k+1 |
| 4 |
| 2k+1 |
| 4 |
| 2k-1 |
| 4(k-1) |
| 2k-1 |
| 4(k-1) |
| 2k-1 |
| 4(k-1) |
| 2k+1 |
| 4 |
| 3-2k |
| 4 |
| 2k-1 |
| 4(k-1) |
| 2k-3 |
| 4(k-1) |
| 1 |
| 2 |
| 3-2k |
| 4 |
| 2k-3 |
| 4(k-1) |
| 1 |
| 8 |
| 1 |
| 4(1-k) |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 4x |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
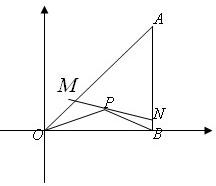
将一块直角三角板ABO置于平面直角坐标系中(如图所示).已知AB=OB=1,AB⊥OB,点P![]() 是三角板内一点.现因三角板中阴影部分受到损坏,要把损坏部分锯掉,可用经过点P的任一直线MN将三角板锯成△AMN.问应如何确定直线MN的斜率,可使锯成的△AMN的面积最大?
是三角板内一点.现因三角板中阴影部分受到损坏,要把损坏部分锯掉,可用经过点P的任一直线MN将三角板锯成△AMN.问应如何确定直线MN的斜率,可使锯成的△AMN的面积最大?

查看答案和解析>>
科目:高中数学 来源:2009-2010学年高三强化班数学寒假作业(直线及其方程)(解析版) 题型:解答题
 是三角板内一点,现因三角板中部分受损坏(△POB),要把损坏的部分锯掉,可用经过P的任意一直线MN将其锯成△AMN,问如何确定直线MN的斜率,才能使锯成的△AMN的面积最大?
是三角板内一点,现因三角板中部分受损坏(△POB),要把损坏的部分锯掉,可用经过P的任意一直线MN将其锯成△AMN,问如何确定直线MN的斜率,才能使锯成的△AMN的面积最大?查看答案和解析>>
科目:高中数学 来源:《直线与方程》2013年山西省高考数学一轮单元复习(解析版) 题型:解答题
 是三角板内一点,现因三角板中部分受损坏(△POB),要把损坏的部分锯掉,可用经过P的任意一直线MN将其锯成△AMN,问如何确定直线MN的斜率,才能使锯成的△AMN的面积最大?
是三角板内一点,现因三角板中部分受损坏(△POB),要把损坏的部分锯掉,可用经过P的任意一直线MN将其锯成△AMN,问如何确定直线MN的斜率,才能使锯成的△AMN的面积最大?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com