[题目]若 {an}是等比数列.a4a7=﹣512.a3+a8=124.且公比q为整数.则a10=( )A.256B.﹣256C.512D.﹣512 题目和参考答案——青夏教育精英家教网—

【题目】若 {an}是等比数列，a4a7=﹣512，a3+a8=124，且公比q为整数，则a10=（）
A.256
B.﹣256
C.512
D.﹣512

【答案】C
【解析】解：{an}是等比数列， ∵a4a7=﹣512，a3+a8=124，
∴a3a8=﹣512，a3+a8=124，
∴a3和a8是方程x2﹣124x﹣512=0的两个实数根，
解方程x2﹣124x﹣512=0，
得x1=128，x2=﹣4，
∵公比q为整数，
∴a3=﹣4，a8=128，
﹣4q5=128，解得q=﹣2，
∴a10=a8（﹣2）2=128×4=512．
故选C．
【考点精析】根据题目的已知条件，利用等比数列的通项公式（及其变式）的相关知识可以得到问题的答案，需要掌握通项公式：．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知f（x）是定义在R上的奇函数，当x≥0时，f（x）=x2﹣3x，则函数g（x）=f（x）﹣x+3的零点的集合为（）
A.{1，3}
B.{﹣3，﹣1，1，3}
C.{2﹣ ，1，3}
D.{﹣2﹣ ，1，3}

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】有下列四个说法：
①若函数f（x）=asinx+cosx（x∈R）的图象关于直线x= 对称，则a= ；
②已知向量 =（1，2）， =（﹣2，m），若与的夹角为钝角，则m＜1；
③当＜α＜时，函数f（x）=sinx﹣logax有三个零点；
④函数f（x）=xsinx在[﹣ ，0]上单调递减，在[0， ]上单调递增．
其中正确的是（填上所有正确说法的序号）

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数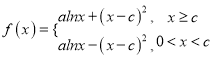（其中，）.

（Ⅰ）当时，若对任意恒成立，求实数的取值范围；

（Ⅱ）设函数的图象在两点、处的切线分别为、，若，，且，求实数的最小值.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】将一枚质地均匀的骰子先后抛掷两次，若第一次朝上一面的点数为a，第二次朝上一面的点数为b，则函数y=ax2﹣2bx+1在（﹣∞，2]上为减函数的概率是．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】直线y=x+b与曲线x= 恰有一个公共点，则b的取值范围是．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】为了培养学生的安全意识，某中学举行了一次安全自救的知识竞赛活动，共有800 名学生参加了这次竞赛．为了解本次竞赛的成绩情况，从中抽取了部分学生的成绩（得分均为整数，满分为100 分）进行统计，得到如下的频率分布表，请你根据频率分布表解答下列问题：

序号（i）	分组（分数）	组中值（Gi）	频数（人数）	频率（Fi）
1	[60，70）	65	①	0.10
2	[70，80）	75	20	②
3	[80，90）	85	③	0.20
4	[90，100）	95	④	⑤
合计			50	1