练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    16．若命题“?x∈R，ax2+2x+1＞0”为真命题，则a的取值范围为（1，+∞）．

    分析 若?x∈R，ax2+2x+1＞0，则对应的二次函数y=ax2+2x+1的图象恒在x轴上方，即开口朝上且与x轴无交点，由此结合二次函数的图象和性质构造关于a的不等式，解不等式可得答案．

    解答 解：∵p（x）：ax2+2x+1＞0，若对?x∈R，p（x）是真命题，
    ①当a=0时，2x+1＞0不恒成立．
    ②当a≠0时，$\left\{\begin{array}{l}{a＞0}\\{△=4-4a＜0}\end{array}\right.$解得a＞1，故实数a的取值范围为（1，+∞），
    故答案为：（1，+∞）

    点评 本题考查的知识点是二次不等式恒成立问题，结合二次函数的图象和性质构造关于a的不等式，是解答的关键．属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    6．设点$A（-2，\sqrt{3}）$，B（2，0），点M在椭圆$\frac{x^2}{16}+\frac{y^2}{12}=1$上运动，当|MA|+|MB|最大时，点M的坐标为8+$\sqrt{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

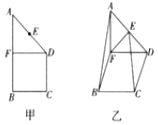    7．如图所示，在直角梯形ABCD中，AB∥CD，∠ABC=90°，CD=BC=1，点E为AD边上的中点，过点D作DF∥BC交AB于点F，现将此直角梯形沿DF折起，使得A-FD-B为直二面角，如图乙所示．
    （1）求证：AB∥平面CEF；
    （2）若AF=$\sqrt{3}$，求点A到平面CEF的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知a，b∈R+，求证：a2+2b2＞2ab+4b-5．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

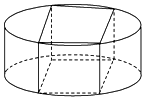    11．将一个底面圆的直径为2、高为1的圆柱截成一个长方体，如图所示，设这个长方体底面的一条边长为x、对角线长为2，底面的面积为A．
    （1）求面积A以x为自变量的函数式；
    （2）求截得长方体的体积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．已知等比数列{an}的前n项和为Sn，2an+2an+2+5Sn=5Sn+1，且a1=q＞1，数列{bn}满足$\frac{{b}_{n}}{{a}_{n}}$=|sin$\frac{（n+1）π}{2}$|．，若数列{bn}的前m项和为340，则m的值为8或9．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．已知变量x，y满足约束条件$\left\{\begin{array}{l}x-y-1≤0\\ 2x-y-3≥0\end{array}\right.$，若目标函数z=ax+2by（a＞0，b＞0）在该约束条件下的最小值为2，则$\frac{1}{a}+\frac{4}{b}$的最小值为9．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．不等式x2-2x-3＜0成立的充要条件是x∈（-1，3）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．已知函数$f（x）=\left\{\begin{array}{l}2x，x＞0\\ f（x+1），x≤0\end{array}\right.$，则$f（-\frac{4}{3}）$=$\frac{4}{3}$，若实数x0满足f（f（x0））=2，则x0的最大值为$\frac{1}{2}$．

    查看答案和解析>>

    同步练习册答案