
【题目】某校为了普及环保知识,增强学生的环保意识,在全校组织了一次有关环保知识的竞赛.经过初赛、复赛,甲、乙两个代表队(每队3人)进入了决赛,规定每人回答一个问题,答对为本队赢得10分,答错得0分.假设甲队中每人答对的概率均为![]() ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为![]() ,
,![]() ,
,![]() ,且各人回答正确与否相互之间没有影响,用
,且各人回答正确与否相互之间没有影响,用![]() 表示乙队的总得分.
表示乙队的总得分.
(Ⅰ)求![]() 的分布列及数学期望;
的分布列及数学期望;
(Ⅱ)求甲、乙两队总得分之和等于30分且甲队获胜的概率.
科目:高中数学 来源: 题型:
【题目】某区的区人大代表有教师6 人,分别来自甲、乙、丙、丁四个学校,其中甲校教师记为![]() ,
,![]() ,乙校教师记为
,乙校教师记为![]() ,
,![]() ,丙校教师记为C,丁校教师记为D.现从这6 名教师代表中选出 3 名教师组成十九大报告宣讲团,要求甲、乙、丙、丁四个学校中,每校至多选出1名.
,丙校教师记为C,丁校教师记为D.现从这6 名教师代表中选出 3 名教师组成十九大报告宣讲团,要求甲、乙、丙、丁四个学校中,每校至多选出1名.
(1)请列出十九大报告宣讲团组成人员的全部可能结果;
(2)求教师![]() 被选中的概率;
被选中的概率;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,直线
,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,且
,且![]() 是
是![]() 的中点.
的中点.
(Ⅰ)求椭圆的离心率;
(Ⅱ)过点![]() 的直线与椭圆相交于
的直线与椭圆相交于![]() 两点,
两点,![]() 都在
都在![]() 轴上方,并且
轴上方,并且![]() 在
在![]() 之间,且
之间,且![]() 到直线
到直线![]() 的距离是
的距离是![]() 到直线
到直线![]() 距离的
距离的![]() 倍.
倍.
①记![]() 的面积分别为
的面积分别为![]() ,求
,求![]() ;
;
②若原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求椭圆方程.
,求椭圆方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四校锥P﹣ABCD中,底面ABCD是菱形,∠BAD=60°,边长为4的正△PAD所在平面与平面ABCD垂直,点E是AD的中点,点Q是侧棱PC的中点.
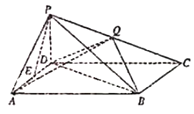
(1)求四棱锥P﹣ABCD的体积;
(2)求证:PA∥平面BDQ;
(3)在线段AB上是否存在点F,使直线PF与平面PAD所成的角为30°?若存在,求出AF的长,若不存在,请说明理由?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知菱形![]() 与直角梯形
与直角梯形![]() 所在的平面互相垂直,其中
所在的平面互相垂直,其中![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点
的中点
(Ⅰ)求证:![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)设![]() 为线段
为线段![]() 上一点,
上一点,![]() ,若直线
,若直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求
,求![]() 的长.
的长.

查看答案和解析>>
科目:高中数学 来源: 题型:
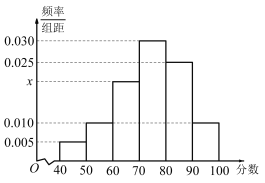
【题目】某校学生社团组织活动丰富,学生会为了解同学对社团活动的满意程度,随机选取了100位同学进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照[40,50),[50,60),[60,70),…,[90,100]分成6组,制成如图所示频率分布直方图.
(1)求图中x的值;
(2)求这组数据的中位数;
(3)现从被调查的问卷满意度评分值在[60,80)的学生中按分层抽样的方法抽取5人进行座谈了解,再从这5人中随机抽取2人作主题发言,求抽取的2人恰在同一组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某汽车公司为调查4S店个数对该公司汽车销量的影响,对同等规模的A,B,C,D四座城市的4S店一个月某型号汽车销量进行了统计,结果如下表:
城市 | A | B | C | D |
4S店个数x | 3 | 4 | 6 | 7 |
销售台数y | 18 | 26 | 34 | 42 |

(1)由散点图知y与x具有线性相关关系,求y关于x的线性回归方程;
(2)根据统计每个城市汽车的盈利![]() (万元)与该城市4S店的个数x符合函数
(万元)与该城市4S店的个数x符合函数![]() ,
,![]() ,为扩大销售,该公司在同等规模的城市E预计要开设多少个4S店,才能使E市的4S店一个月某型号骑车销售盈利达到最大,并求出最大值.
,为扩大销售,该公司在同等规模的城市E预计要开设多少个4S店,才能使E市的4S店一个月某型号骑车销售盈利达到最大,并求出最大值.
附:回归方程![]() 中的斜率和截距的最小二乘法估计公式分别为:
中的斜率和截距的最小二乘法估计公式分别为: ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
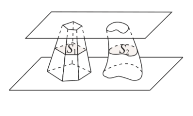
【题目】南北朝时代的伟大科学家祖暅在数学上有突出贡献,他在实践的基础上提出祖暅原理:“幂势既同,则积不容异”. 其含义是:夹在两个平行平面之间的两个几何体,被平行于这两个平行平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等.如图,夹在两个平行平面之间的两个几何体的体积分别为![]() ,被平行于这两个平面的任意平面截得的两个截面面积分别为
,被平行于这两个平面的任意平面截得的两个截面面积分别为![]() ,则“
,则“![]() 相等”是“
相等”是“![]() 总相等”的
总相等”的
A. 充分而不必要条件B. 必要而不充分条件
C. 充分必要条件D. 既不充分也不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com