
【题目】已知圆锥的顶点为A,高和底面的半径相等,BE是底面圆的一条直径,点D为底面圆周上的一点,且∠ABD=60°,则异面直线AB与DE所成角的正弦值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
根据圆锥高和底面的半径相等,且点D为底面圆周上的一点,∠ABD=60,可知D为![]() 的中点,则以底面中心为原点,分别以OD,OE,OA为x,y,z轴,建立空间直角坐标系,不妨设底面半径为1,求得向量
的中点,则以底面中心为原点,分别以OD,OE,OA为x,y,z轴,建立空间直角坐标系,不妨设底面半径为1,求得向量![]() ,
,![]() 的坐标,代入公式cos
的坐标,代入公式cos![]() ,
,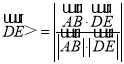 求解.
求解.
因为高和底面的半径相等,∴OE=OB=OA,OA⊥底面DEB.
∵点D为底面圆周上的一点,且∠ABD=60°,
∴AB=AD=DB;
∴D为![]() 的中点
的中点
建立如图所示空间直角坐标系,
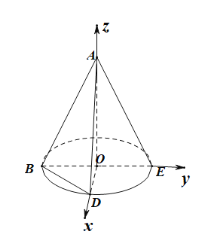
不妨设OB=1.
则O(0,0,0),B(0,﹣1,0),D(1,0,0),A(0,0,1),E(0,1,0),
∴![]() (0,﹣1,﹣1),
(0,﹣1,﹣1),![]() (﹣1,1,0),
(﹣1,1,0),
∴cos![]() ,
,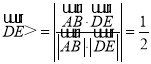 ,
,
∴异面直线AM与PB所成角的大小为![]() .
.
∴异面直线AB与DE所成角的正弦值为![]() .
.
故选:A.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() :
:![]() ,直线
,直线![]() :
:![]() .以极点
.以极点![]() 为原点,极轴为
为原点,极轴为![]() 轴的正半轴建立平面直角坐标系.
轴的正半轴建立平面直角坐标系.
(1)求直线![]() ,
,![]() 的直角坐标方程以及曲线
的直角坐标方程以及曲线![]() 的参数方程;
的参数方程;
(2)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,直线
两点,直线![]() 与曲线C交于
与曲线C交于![]() ,
,![]() 两点,求
两点,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 分别在线段
分别在线段![]() 和
和![]() 上,且
上,且![]() ,
,![]() 为
为![]() 中点,以
中点,以![]() 为折痕将
为折痕将![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置,且平面
的位置,且平面![]() 平面
平面![]() .
.
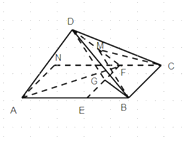
(1)求证:平面![]() 平面
平面![]() ;
;
(2)点![]() 为线段
为线段![]() 的中点,求三棱锥
的中点,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c为正数,f(x)=|x+a|+|x+b|+|x﹣c|.
(1)若a=b=c=1,求函数f(x)的最小值;
(2)若f(0)=1且a,b,c不全相等,求证:b3c+c3a+a3b>abc.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数![]() 在
在![]() ,
,![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围;
的取值范围;
(2)若函数![]() 在
在![]() 处的切线平行于
处的切线平行于![]() 轴,是否存在整数
轴,是否存在整数![]() ,使不等式
,使不等式![]() 在
在![]() 时恒成立?若存在,求出
时恒成立?若存在,求出![]() 的最大值;若不存在,请说明理由.
的最大值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点F为椭圆![]() (a>b>0)的一个焦点,点A为椭圆的右顶点,点B为椭圆的下顶点,椭圆上任意一点到点F距离的最大值为3,最小值为1.
(a>b>0)的一个焦点,点A为椭圆的右顶点,点B为椭圆的下顶点,椭圆上任意一点到点F距离的最大值为3,最小值为1.
(1)求椭圆的标准方程;
(2)若M、N在椭圆上但不在坐标轴上,且直线AM∥直线BN,直线AN、BM的斜率分别为k1和k2,求证:k1k2=e2﹣1(e为椭圆的离心率).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甘肃省是土地荒漠化较为严重的省份,一代代治沙人为了固沙、治沙,改善生态环境,不断地进行研究与实践,实现了沙退人进.![]() 年,古浪县八步沙林场“六老汉”三代人治沙群体作为优秀代表,被中宣部授予“时代楷模”称号.在治沙过程中为检测某种固沙方法的效果,治沙人在某一实验沙丘的坡顶和坡腰各布设了
年,古浪县八步沙林场“六老汉”三代人治沙群体作为优秀代表,被中宣部授予“时代楷模”称号.在治沙过程中为检测某种固沙方法的效果,治沙人在某一实验沙丘的坡顶和坡腰各布设了![]() 个风蚀插钎,以测量风蚀值.(风蚀值是测量固沙效果的指标之一,数值越小表示该插钎处被风吹走的沙层厚度越小,说明固沙效果越好,数值为
个风蚀插钎,以测量风蚀值.(风蚀值是测量固沙效果的指标之一,数值越小表示该插钎处被风吹走的沙层厚度越小,说明固沙效果越好,数值为![]() 表示该插钎处没有被风蚀)通过一段时间的观测,治沙人记录了坡顶和坡腰全部插钎测得的风蚀值(所测数据均不为整数),并绘制了相应的频率分布直方图.
表示该插钎处没有被风蚀)通过一段时间的观测,治沙人记录了坡顶和坡腰全部插钎测得的风蚀值(所测数据均不为整数),并绘制了相应的频率分布直方图.
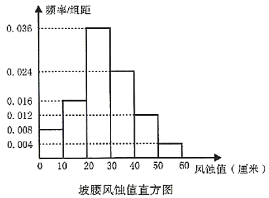
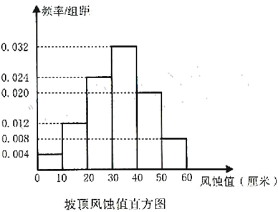
(Ⅰ)根据直方图估计“坡腰处一个插钎风蚀值小于![]() ”的概率;
”的概率;
(Ⅱ)若一个插钎的风蚀值小于![]() ,则该数据要标记“
,则该数据要标记“![]() ”,否则不标记根据以上直方图,完成列联表:
”,否则不标记根据以上直方图,完成列联表:
标记 | 不标记 | 合计 | |
坡腰 | |||
坡顶 | |||
合计 |
并判断是否有![]() 的把握认为数据标记“
的把握认为数据标记“![]() ”与沙丘上插钎所布设的位置有关?
”与沙丘上插钎所布设的位置有关?
附: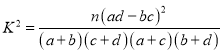 .
.
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市在进行创建文明城市的活动中,为了解居民对“创建文明城”的满意程度,组织居民给活动打分(分数为整数,满分100分),从中随机抽取一个容量为120的样本,发现所给数据均在[40,100]内.现将这些分数分成以下6组并画出样本的频率分布直方图,但不小心污损了部分图形,如图所示.观察图形则下列说法中有错误的是( )
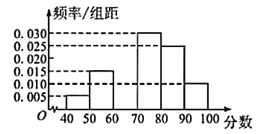
A.第三组的频数为18人
B.根据频率分布直方图估计众数为75分
C.根据频率分布直方图估计样本的平均数为75分
D.根据频率分布直方图估计样本的中位数为75分
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com