[题目]已知函数..其中且.(1)求函数的定义域,(2)若函数的最大值是2.求的值,(3)求使成立的的取值范围. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】已知函数，，其中且.

（1）求函数的定义域；

（2）若函数的最大值是2，求的值；

（3）求使成立的的取值范围.

【答案】（1）（2）（3）时满足题意的的取值范围是;时满足题意的的取值范围是

【解析】

（1）根据对数函数的性质，真数大于0，可得函数定义域；（2）利用对数的运算法则将进行化简，转为复合函数求最值问题；

（3）不等式f（x）＞g（x），即loga（x+2）＞loga（4﹣x），利用对数的性质及运算，对底数a进行讨论，可得答案．

（1）要使的表达式有意义，

则有：

∴函数的定义域是

（2）令，

则

设，则，

∵函数的最大值是2.

即，的最大值是2.

∴且，∴

∴

（3）由即

Ⅰ：若，则,∴

Ⅱ：若，则有：,∴

∴时满足题意的的取值范围是

时满足题意的的取值范围是.

练习册系列答案

新路学业快乐假期寒假总复习系列答案

举一反三期末百分冲刺卷系列答案

假期生活寒假方圆电子音像出版社系列答案

百年学典快乐假期寒假作业系列答案

复习大本营期末假期复习一本通寒假系列答案

五州图书超越假期寒假系列答案

特优复习计划期末冲刺寒假作业教材衔接系列答案

中考热点试题分类全解系列答案

必做题1000例考前冲刺必备中考系列答案

天勤文化寒假攻略光明日报出版社系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知函数f（x）=lnx+ax在点（t，f（t））处的切线方程为y=3x+1
（1）求a的值；
（2）已知k≤2，当x＞1时，f（x）＞k（1﹣ ）+2x﹣1恒成立，求实数k的取值范围；
（3）对于在（0，1）中的任意一个常数b，是否存在正数x0 ，使得e + x02＜1？请说明理由．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，△ABC是圆的内接三角形，∠BAC的平分线交圆于点D，交BC于E，过点B的圆的切线与AD的延长线交于点F，在上述条件下，给出下列四个结论：
①BD平分∠CBF；
②FB2=FDFA；
③AECE=BEDE；
④AFBD=ABBF．

所有正确结论的序号是（）
A.①②
B.③④
C.①②③
D.①②④

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】[选修4-1：几何证明选讲]
如图，在正方形ABCD中，E，G分别在边DA，DC上（不与端点重合），且DE=DG，过D点作DF⊥CE，垂足为F．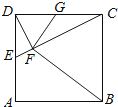

（1）证明：B，C，G，F四点共圆；
（2）若AB=1，E为DA的中点，求四边形BCGF的面积．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某大学生在开学季准备销售一种文具套盒进行试创业，在一个开学季内，每售出盒该产品获利润元；未售出的产品，每盒亏损元.根据历史资料，得到开学季市场需求量的频率分布直方图，如图所示。该同学为这个开学季购进了盒该产品，以(单位：盒，)表示这个开学季内的市场需求量，(单位：元)表示这个开学季内经销该产品的利润。