【答案】
分析:(Ⅰ)由题意求出f′(x),再求出f′(0)和f(0)的值,代入点斜式进行化简,化为一般式方程;
(Ⅱ)先构造函数g(x)=f′(x),再将题意转化为x
1,x
2是方程g(x)=0的两个实根,再求出g′(x),对a进行分类分别求出g(x)的单调区间以及最大值,再令最大值大于零,列出关于a的不等式求解;
(Ⅲ)由题意先构造函数h(x)=e
x-ax
2-x-1,转化为h(x)≥0在[0,+∞)恒成立问题,再求出h(x)的单调性和最小值,关键是对a进行分类后,得到“当a=0时,e
x≥1+x”这一结论在后面的应用.
解答:心理年龄解:(Ⅰ)由题意得,当a=1时,f(x)=x
2-e
x,
∴f′(x)=2x-e
x,则切线的斜率为f′(0)=-1,
∵f(0)=-e
=-1,
∴所求的切线方程为:x+y+1=0;
(Ⅱ)设g(x)=f′(x)=2ax-e
x,
由题意得,x
1,x
2是方程g(x)=0(即2ax-e
x=0)的两个实根,
则g′(x)=2a-e
x,
当a≤0时,g′(x)<0,g(x)在定义域上递减,即方程g(x)=0不可能有两个实根,
当a>0时,由g′(x)=0,得x=ln2a,
当x∈(-∞,ln2a)时,g′(x)>0,则g(x)在(-∞,ln2a)上递增,
当x∈(ln2a,+∞)时,g′(x)<0,则g(x)在(-∞,ln2a)上递减,
∴g
max(x)=g(ln2a)=2aln2a-2a,
∵方程g(x)=0(即2ax-e
x=0)有两个实根,
∴2aln2a-2a>0,解得2a>e即
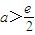
,
(Ⅲ)设h(x)=e
x-ax
2-x-1,则由题意得h(x)=e
x-ax
2-x-1≥0在[0,+∞)恒成立,
则h′(x)=e
x-2ax-1,
当a=0时,h′(x)≥0,h(x)在[0,+∞)上单调递增,
∴h(x)≥h(0)=0,即e
x≥1+x,当且仅当x=0时,等号成立,
∴h′(x)=e
x-2ax-1≥1+x-2ax-1=x(1-2a),
当1-2a≥0时,即a≤

,此时h′(x)≥0,h(x)在[0,+∞)上单调递增,
∴h(x)≥h(0)=e
-0-1=0,即h(x)≥0,
因而a≤

时,h(x)≥0,
下面证明a>

时的情况:
由e
x≥1+x得,e
-x≥1-x,即x≥1-e
-x,
∴h′(x)=e
x-1-2ax≤e
x-1-2a(1-e
-x)=e
-x(e
x-1)(e
x-2a)
当e
x<2a时,即0<x<ln2a,则当x∈(0,ln2a)时,h′(x)<0,从而h(x)<0,
因此,对于x≥0,f(x)≤-x-1不恒成立,
综上所得,a的最大值为

.
点评:本题考查了导数的几何意义,方程的根与函数零点的关系,导数与函数的单调性、极值、最值的综合应用,考查了转化思想、分类讨论思想以及分析、解决问题的能力.

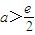 ,
, ,此时h′(x)≥0,h(x)在[0,+∞)上单调递增,
,此时h′(x)≥0,h(x)在[0,+∞)上单调递增, 时,h(x)≥0,
时,h(x)≥0, 时的情况:
时的情况: .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案