
| 2 |
| 2 |
| b |
| x |
| b |
| x |
| b |
| x |
| b |
| x |
| b |
| x |
| 2 |
| b |
| x |
| b |
| x |
| b |
| x |
|
| b |
| x |
| b |
| x |
| b |
| x |
| -b |
| x |
| -b |
| -b |
| b |
| x |
| -b |
| b |
| x |
| 6 |
| -b |
|
| 2 |
| 2 |
| -b |
| b |
| x |
|
| 2 |
| -b |


科目:高中数学 来源: 题型:
 以下给出的是用条件语句编写的一个程序,根据该程序回答:
以下给出的是用条件语句编写的一个程序,根据该程序回答:
|
|
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:022
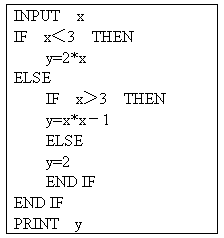
以下给出的是用条件语句编写的一个程序,根据该程序回答:
(1)若输入4,则输出结果是________;
(2)该程序的功能是求函数________的函数值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
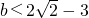 ,若在[0,1]随机输入x,则输出的y值为负,求实数a的取值范围.
,若在[0,1]随机输入x,则输出的y值为负,求实数a的取值范围.查看答案和解析>>
科目:高中数学 来源:2008-2009学年江苏省南通中学高二(上)期中数学试卷(解析版) 题型:解答题
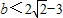 ,若在[0,1]随机输入x,则输出的y值为负,求实数a的取值范围.
,若在[0,1]随机输入x,则输出的y值为负,求实数a的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com