
| ||
| 6 |
| ||
| 6 |
 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源:学习周报 数学 北师大课标高二版(选修1-2) 2009-2010学年 第32期 总第188期 北师大课标 题型:022
在边长为a的正三角形内任取一点P,设它到三边的距离分别为r1,r2,r3,连接PA,PB,PC,利用三角形面积公式S△ABC=![]() a2=
a2=![]() (r1+r2+r3)a,可得正三角形内任一点到三边的距离之和是一个定值,即r1+r2+r3=
(r1+r2+r3)a,可得正三角形内任一点到三边的距离之和是一个定值,即r1+r2+r3=![]() a.类比到棱长为a的正四面体内一点P,它到正四面体各面的距离之和是定值________.
a.类比到棱长为a的正四面体内一点P,它到正四面体各面的距离之和是定值________.
查看答案和解析>>
科目:高中数学 来源:2011年云南省高三第二次复习统测数学试卷(理科)(解析版) 题型:选择题
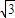 的正四面体内,如果球0是该正四面体内的最大球,那么球O的表面积等于( )
的正四面体内,如果球0是该正四面体内的最大球,那么球O的表面积等于( )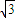 π
π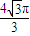
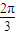
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com