
����Ŀ��ij��ѧ���ѡȡ��![]() �������������ǵ�������Ϊ��������ͳ�ƣ��õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ���۲�ͼ�����ݣ�����������⣮
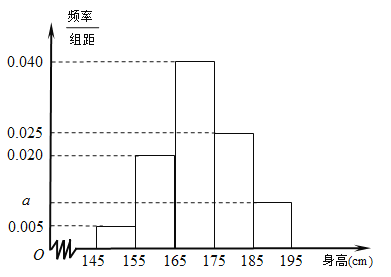
�������������ǵ�������Ϊ��������ͳ�ƣ��õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ���۲�ͼ�����ݣ�����������⣮
������![]() ��ֵ������������������
��ֵ������������������![]() ����λ:
����λ: ![]() ����������
����������
����������ͬһ���е�ÿ�����ݿ��ø���������е�ֵ���棬ͨ���������Ƹ�Уȫ��������ƽ�����ߣ�
��������������������![]() ��
��![]() ����λ:
����λ: ![]() ���ڵ���������ѡ���ˣ��������˵����߶�������
���ڵ���������ѡ���ˣ��������˵����߶�������![]() �ĸ��ʣ�
�ĸ��ʣ�
���𰸡���1��![]() ��2��
��2��![]() ��3��
��3��![]()
�������������������1������Ƶ��ֱ��ͼ�������Ϊ1�������![]() ,n=N*��*���
,n=N*��*���![]() ����2��ƽ����Ϊ��ÿ��������е�ֵ��Ƶ�ʳ˻��͡�
����2��ƽ����Ϊ��ÿ��������е�ֵ��Ƶ�ʳ˻��͡�
��3��ѧ��������![]() �ڵ�����
�ڵ�����![]() ������������Ϊ
������������Ϊ![]() �����ԣ�������
�����ԣ�������![]() ��
��![]() �ڵ�������
�ڵ�������![]() �ˡ�����ö�ٿɵ��ܹ�15�������¼����������6����
�ˡ�����ö�ٿɵ��ܹ�15�������¼����������6����![]() ��
��
������������������⣬ ![]() .
.
��� ![]() ��
��
����������ѧ��������![]() �ڣ���λ:
�ڣ���λ: ![]() ��������Ϊ
��������Ϊ
![]() ��
��
�������������������ߵ�ƽ��ֵΪ![]() ����
����
![]()
![]() ��
��
���ԣ���У������ƽ������Ϊ![]() ��
��
��������������������![]() �ڵ�����
�ڵ�����
![]() ����������������Ϊ
����������������Ϊ![]() ��
��
�ɣ���֪��ѧ��������![]() �ڵ�����
�ڵ�����![]() ������������Ϊ
������������Ϊ![]() ��
��
���ԣ�������![]() ��
��![]() �ڵ�������
�ڵ�������![]() �ˣ�
�ˣ�
����![]() ��������ѡȡ
��������ѡȡ![]() �ˣ���
�ˣ���![]() ��
��
��![]() �������
�������
����ѡ���˵����߶�������![]() Ϊ�¼�
Ϊ�¼�![]() ���¼�
���¼�![]() ����
����![]() ����
����![]() �������
�������
���ԣ���ѡ���˵����߶�������![]() �ĸ���Ϊ
�ĸ���Ϊ![]() ��
��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��3��������һ��6����λ�ϣ��ʣ�
��1��3���˶����ڵ������ж����֣�
��2����λ�������ڵ������ж����֣�
��3����λ������2�����ڵ������ж����֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
����������![]() ��
��![]() ��������
��������![]() ��ֱ��
��ֱ��![]() ��ֱ����
��ֱ����![]() ��ֵ��
��ֵ��
����![]() ʱ����֤������ʵ��
ʱ����֤������ʵ��![]() ʹ
ʹ![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=ex �� ����ʵ��m��n��p��f��m+n��=f��m��+f��n����f��m+n+p��=f��m��+f��n��+f��p������p�����ֵ���� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
�� ![]()
![]() ��
��
������ֱ��![]()
![]() ������
������![]() ��
��![]() �ֱ���
�ֱ���![]() ����.������
����.������
![]() �ڵ�
�ڵ�![]() ��������Ϊ
��������Ϊ![]() ��
�� ![]() �ڵ�
�ڵ�![]() ��������Ϊ
��������Ϊ![]() .
.
��������![]() ʱ����
ʱ����![]()
![]() ����
����![]() ��ֵ��
��ֵ��
��������![]() ����
����![]() �����ֵ��
�����ֵ��
�����躯��![]() ���䶨������ǡ��������ͬ�ļ�ֵ��
���䶨������ǡ��������ͬ�ļ�ֵ��![]() ��
�� ![]() ����
����![]() ��
��
��![]() ����
����![]() ���������
���������![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}��ǰn���ΪSn �� a1=�� ![]() ��Sn+
��Sn+ ![]() =an��2��n��2��n��N��
=an��2��n��2��n��N��
��1����S2 �� S3 �� S4��ֵ��
��2������Sn�ı���ʽ��������ѧ���ɷ�����֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ⳤΪ1��������ABCDA1B1C1D1�У�EΪ��BC���е㣬��F����CD�ϵĶ��㣬��ȷ����F��λ�ã�ʹ��D1E��ƽ��AB1F�� 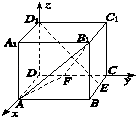
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�������������ѧ�ɼ���ѧ������ѧϰʱ��֮�����ع�ϵ��������ѧ��ѧ��ʦ������ѧ��45��ѧ�������˸��ٵ��飬����ÿ����������ѧ���ʱ�䲻����15Сʱ����19�ˣ����µ����У��ڸ���ģ�⿼������ѧƽ���ɼ�����120�ֵ�ռ![]() ��ͳ�Ƴɼ��õ����µ�
��ͳ�Ƴɼ��õ����µ�![]() ��������
��������
�������ڵ���120�� | ��������120�� | �ϼ� | |
������ʱ�䲻����15Сʱ | 4 | 19 | |
������ʱ�䲻��15Сʱ | |||
�ϼ� | 45 |
��1������������![]() �����������ж��ܷ��ڷ�����ĸ��ʲ�����0.01��ǰ������Ϊ������������ѧ�ɼ���ѧ������ѧϰʱ���йء���
�����������ж��ܷ��ڷ�����ĸ��ʲ�����0.01��ǰ������Ϊ������������ѧ�ɼ���ѧ������ѧϰʱ���йء���
��2�����������շֲ�����ķ����������������У��ӷ������ڵ���120�ֺͷ�������120������ѧ���г�ȡ9��ѧ������鵽�IJ���120����������ʱ�䲻��15Сʱ��������![]() ����
����![]() �ķֲ��У��������������ʽ��ʾ����
�ķֲ��У��������������ʽ��ʾ����
����������Ƶ����Ϊ���ʣ���ȫУ���ڵ���120�ֵ�ѧ���������ȡ20�ˣ�����Щ����������ʱ�䲻����15Сʱ�������������ͷ���.
|
|
|
|
|
|
|
|
���� 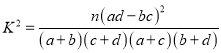
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڳ�����ABCD��A1B1C1D1�У�AA1=AD=1��EΪCD�е㣮 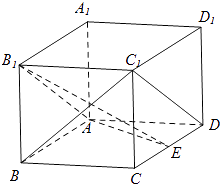
��1����֤��C1D��ƽ��AB1E��
��2����֤��BC1��B1E��
��3����AB= ![]() ��������E��AB1��B������ֵ��
��������E��AB1��B������ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com