
分析 (1)由已知中,x∈(-∞,0]时的解析式为f(x)=x2+2x,我们可由x>0时,-x<0,代入求出f(-x),进而根据y=f(x)是偶函数,得到x>0时,f(x)的解析式;
(2)根据分段函数分段画的原则,结合(1)中函数的解析式,我们易画出函数的图象,结合图象,我们根据从左到右图象上升,函数为增函数,图象下降,函数为减函数的原则,得到函数的单调性.
解答 解:(1)当x>0时,-x<0,f(-x)=(-x)2-2x=x2-2x
又f(x)为偶函数,∴f(-x)=f(x)
∴f(x)=x2-2x
∴$f(x)=\left\{\begin{array}{l}{x^2}-2x,x>0\\{x^2}+2x,x≤0\end{array}\right.$…(6分)
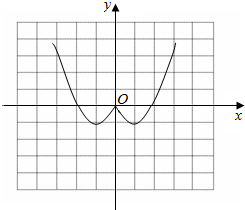
(2)
…(9分)
单调递增区间为:(-1,0),(1,+∞)
单调递减区间为:(0,1),(-∞,-1)…(13分)
点评 本题考查的知识点是偶函数,函数解析式的求解,函数图象的作法,图象法判断函数的单调性,其中根据偶函数的性质,求出函数的解析式是解答本题的关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3e | B. | -1 | C. | -e3 | D. | e2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com