
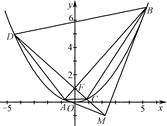
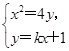 消去y,得x2-4kx-4=0,显然Δ=16k2+16>0.
消去y,得x2-4kx-4=0,显然Δ=16k2+16>0.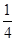 x2,所以y′=
x2,所以y′=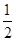 x,所以,直线AM的斜率为kAM=
x,所以,直线AM的斜率为kAM=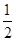 x1,
x1,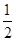 x1(x-x1),又
x1(x-x1),又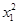 =4y1,
=4y1,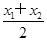 ,即A、M、B三点的横坐标成等差数列.
,即A、M、B三点的横坐标成等差数列.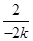 =-
=-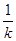 ,则直线MF的方程为y=-
,则直线MF的方程为y=-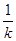 x+1,
x+1,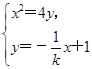 消去y,得x2+
消去y,得x2+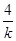 x-4=0,显然Δ=
x-4=0,显然Δ=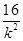 +16>0,
+16>0,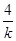 ,x3x4=-4,又|AB|=
,x3x4=-4,又|AB|=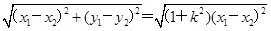
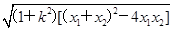 =4(k2+1),
=4(k2+1),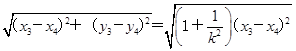 =
=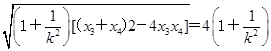 ,
,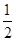 |AB|·|CD|=8
|AB|·|CD|=8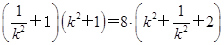 ≥32,
≥32,

 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:高中数学 来源:不详 题型:解答题
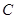 上任意一点
上任意一点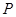 作直线
作直线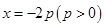 的垂线,垂足为
的垂线,垂足为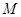 ,且
,且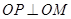 .
.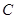 的方程;
的方程;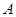 、
、 是曲线
是曲线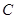 上两个不同点,直线
上两个不同点,直线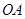 和
和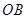 的倾斜角分别为
的倾斜角分别为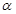 和
和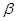 ,
,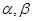 变化且
变化且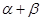 为定值
为定值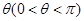 时,证明直线
时,证明直线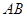 恒过定点,
恒过定点,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com