
【题目】已知函数![]() .
.
(1)求函数![]() 的极值.
的极值.
(2)![]() ,若不等式
,若不等式![]() 在
在![]() 上恒成立,求
上恒成立,求![]() 的最大值.
的最大值.
(3)是否存在实数![]() ,使得函数
,使得函数![]() 在
在![]() 上的值域为
上的值域为![]() ?如果存在,请给出证明;如果不存在,请说明理由.
?如果存在,请给出证明;如果不存在,请说明理由.
【答案】(1)极大值![]() 没有极小值;(2)最大值为
没有极小值;(2)最大值为![]() ;(3)存在,见解析
;(3)存在,见解析
【解析】
(1)先求出![]() ,令
,令![]() ,再列表讨论
,再列表讨论![]() 的单调区间,进而可求出函数的极值;(2)根据不等式构造函数
的单调区间,进而可求出函数的极值;(2)根据不等式构造函数![]() ,求导并判断单调性,进而可求出
,求导并判断单调性,进而可求出![]() 的最大值;
的最大值;
(3)由(1)知,当![]() 时,
时,![]() ,得
,得![]() ,结合函数
,结合函数![]() 的单调性可猜想,存在实数
的单调性可猜想,存在实数![]() 符合题意,其中
符合题意,其中![]() ,
,![]() 为
为![]() 的图象与直线
的图象与直线![]() 在
在![]() 上的交点的横坐标,再证明
上的交点的横坐标,再证明![]() 在
在![]() 上只有一个实数解即可.
上只有一个实数解即可.
(1)![]() ,其定义域为
,其定义域为![]() ,
,
求导得![]() .
.
令![]() ,得
,得![]() .
.
![]() 的关系列表如下:
的关系列表如下:
|
| 1 |
|
| + | 0 |
|
| ↗ | 极大值 | ↘ |
因此,当![]() 时,
时,![]() 取得极大值
取得极大值![]() 没有极小值.
没有极小值.
(2)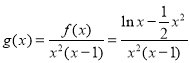 ,
,
因为![]() 在
在![]() 上恒成立,
上恒成立,
所以![]() 在
在![]() 上恒成立,
上恒成立,
设![]() ,
,
则原问题转化为![]() 在
在![]() 上恒成立.
上恒成立.
![]() ,
,
令![]() ,解得
,解得![]() .
.
![]() 的关系列表如下:
的关系列表如下:
|
|
|
|
| + | 0 |
|
| ↗ | 极大值 | ↘ |
所以只需![]() ,故
,故![]() 的最大值为
的最大值为![]() .
.
(3)存在实数![]() ,满足题意.
,满足题意.
证明如下:
由(1)知,当![]() 时,
时,![]() ,
,
所以![]() ,即
,即![]() ,注意到
,注意到![]() 在
在![]() 上单调递减,
上单调递减,
结合函数![]() 的单调性可猜想,存在实数
的单调性可猜想,存在实数![]() 符合题意,其中
符合题意,其中![]() ,
,![]() 为
为![]() 的图象与直线
的图象与直线![]() 在
在![]() 上的交点的横坐标.
上的交点的横坐标.
故只需证明方程![]() 在
在![]() 上只有一个实数解.
上只有一个实数解.
令![]() ,则
,则![]() ,
,
令![]() ,得
,得![]() ,因为
,因为![]() ,所以只有
,所以只有![]() 成立.
成立.
![]() 的关系列表如下:
的关系列表如下:
|
|
|
|
| + | 0 |
|
| ↗ | 极大值 | ↘ |
因为![]() ,所以当
,所以当![]() 时,
时,![]() ,
,
又![]() ,
,
所以存在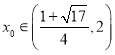 ,使得
,使得![]() ,满足
,满足![]() ,
,
因为函数![]() 在
在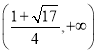 上单调递减,所以方程
上单调递减,所以方程![]() 在
在![]() 上只有一个实数解.
上只有一个实数解.
综上所述,存在实数![]() ,使得函数
,使得函数![]() 在
在![]() 上的值域为
上的值域为![]() .
.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:
【题目】某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图(如图①)、90后从事互联网行业岗位分布条形图(如图②),则下列结论中不一定正确的是( )
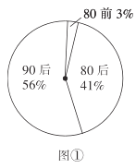
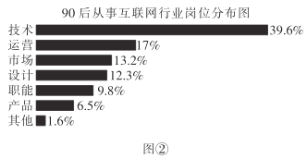
注:90后指1990年及以后出生,80后指1980~1989年之间出生,80前指1979年及以前出生.
A.互联网行业从业人员中90后占一半以上
B.互联网行业中从事技术岗位的人数超过总人数的20%
C.互联网行业中从事运营岗位的人数90后比80前多
D.互联网行业中从事技术岗位的人数90后比80后多
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解某高校全校学生的阅读情况,随机调查了200名学生每周阅读时间![]() (单位:小时)并绘制如图所示的频率分布直方图.
(单位:小时)并绘制如图所示的频率分布直方图.
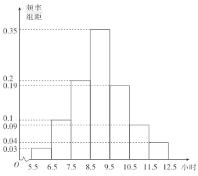
(1)求这200名学生每周阅读时间的样本平均数![]() 和中位数
和中位数![]() (
(![]() 的值精确到0.01);
的值精确到0.01);
(2)为查找影响学生阅读时间的因素,学校团委决定从每周阅读时间为![]() ,
,![]() 的学生中抽取9名参加座谈会.你认为9个名额应该怎么分配?并说明理由.
的学生中抽取9名参加座谈会.你认为9个名额应该怎么分配?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,且x=0是f(x)的极值点.
,且x=0是f(x)的极值点.
(1)求f(x)的最小值;
(2)是否存在实数b,使得关于x的不等式ex<bx+f(x)在(0,+∞)上恒成立?若存在,求出b的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 过点
过点![]() ,
,![]() 、
、![]() 分别为椭圆C的左、右焦点且
分别为椭圆C的左、右焦点且![]()
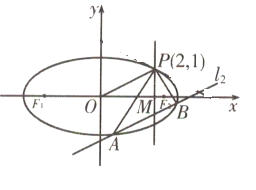
(1)求椭圆C的方程;
(2)直线![]() 平行于OP(O为原点),且与椭圆C交于两点A、B,与直线x=2交于点M(M介于A、B两点之间).
平行于OP(O为原点),且与椭圆C交于两点A、B,与直线x=2交于点M(M介于A、B两点之间).
(I)当△PAB面积最大时,求![]() 的方程;
的方程;
(II)求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com