练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．如图，渔船甲位于岛屿A的南偏西60°方向的B处，且与岛屿A相距12海里，渔船乙以10海里/小时的速度从岛屿A出发沿正北方向航行，若渔船甲同时从B出发沿北偏东α的方向追赶渔船乙，刚好用两小时追赶上．
    （1）求渔船甲的速度；
    （2）求sinC的值．

    分析 （1）由题意推出∠BAC=120°，利用余弦定理求出BC=28，然后推出渔船甲的速度；
    （2）在△ABC中，直接利用正弦定理求出sinC．

    解答 解：（1）依题意，∠BAC=120°，AB=12海里，AC=20海里．
    在ABC中，由余弦定理得，得BC2=AB2+AC2-2AB×AC×cos∠BAC．
    =122+202-2×12×20×cos120°=784．
    解得BC=28海里，所以渔船甲的速度是=14（海里/小时）
    （2）在三角形ABC中，因为AB=12海里，∠BAC=120°，BC=28海里，
    由正弦定理，得sinC=$\frac{ABsin120°}{BC}$=$\frac{3\sqrt{3}}{14}$．

    点评 本题是中档题，考查三角函数在实际问题中的应用，正弦定理、余弦定理的应用，考查计算能力．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    2．已知f（x）=x+xlnx，若k（x-2）＜f（x）对任意x＞2恒成立，则整数k的最大值是（　　）
    A．8B．6C．5D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

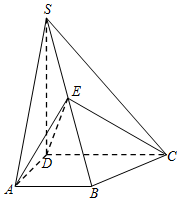    20．如图，在四棱锥S-ABCD中，已知SD⊥底面ABCD，且四边形ABCD为直角梯形，∠DAB=∠ADC=$\frac{π}{2}$，SD=DC=2，AD=AB=1，E为棱SB上的一点，且DE⊥SC．
    （Ⅰ）求$\frac{SE}{EB}$的值；
    （Ⅱ）求直线EC与平面ADE所成角．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．若A、B、C、D四人站成一排照相，A、B相邻的排法总数为k，则二项式${（{1-\frac{x}{k}}）^k}$的展开式中含x2项的系数为$\frac{11}{24}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．若数f（x）=lnx+x2+ax（a∈R）
    （1）若函数f（x）的图象在点P（1，f（1））处的切线与直线x+2y-1=0垂直，求实数a的值；
    （2）求函数f（x）的单调区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

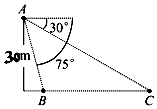    14．如图，从气球A上测得正前方的河流的两岸B，C的俯角分别为75°，30°，此时气球的高是30m，则河流的宽度BC等于$60（\sqrt{3}-1）$m．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．设函数f（x）=lnx+$\frac{a}{ex}$
    （Ⅰ）求函数f（x）的单调区间；
    （Ⅱ）若a=2，证明：对任意的实数x＞0，都有f（x）＞e-x．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．设两个独立事件A和B都不发生的概率为$\frac{1}{9}$，A发生B不发生的概率与B发生A不发生的概率相同，则事件A发生的概率P（A）是$\frac{2}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．已知向量$\overrightarrow a=（{-2，2}）$，$\overrightarrow b=（{5，m}）$，且|$\overrightarrow a+\overrightarrow b|$不超过5，则函数f（x）=$\sqrt{3}$cosx-sinx+m有零点的概率是（　　）
    A．$\frac{3}{4}$B．$\frac{2}{3}$C．$\frac{3}{5}$D．$\frac{1}{2}$

    查看答案和解析>>

    同步练习册答案