
【题目】在直角坐标系内,已知 ![]() 是圆
是圆 ![]() 上一点,折叠该圆两次使点
上一点,折叠该圆两次使点 ![]() 分别与圆上不相同的两点(异于点
分别与圆上不相同的两点(异于点 ![]() )重合,两次的折痕方程分别为
)重合,两次的折痕方程分别为 ![]() 和
和 ![]() ,若圆
,若圆 ![]() 上存在点
上存在点 ![]() ,使
,使 ![]() ,其中
,其中 ![]() 的坐标分别为
的坐标分别为 ![]() ,则实数
,则实数 ![]() 的取值集合为 .
的取值集合为 .
【答案】![]()
【解析】由题意,∴A(3,2)是⊙C上一点,折叠该圆两次使点A分别与圆上不相同的两点(异于点A)重合,两次的折痕方程分别为x﹣y+1=0和x+y﹣7=0,
∴圆上不相同的两点为B(1,4),D(5,4),
∵A(3,2),BA⊥DA
∴BD的中点为圆心C(3,4),半径为1,
∴⊙C的方程为(x﹣3)2+(y﹣4)2=4.
过P,M,N的圆的方程为x2+y2=m2 ,
∴两圆外切时,m的最大值为 ![]() ,两圆内切时,m的最小值为
,两圆内切时,m的最小值为 ![]() ,
,
故答案为[3,7].
根据已知条件求出圆心C的坐标和半径,然后求出圆的方程,可知过点P、M、N的圆的方程,两圆外切时,m取得最大值,两圆内切时,m取得最小值,进而求出m的取值集合。


科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2+2x-4y+3=0.
(1)若圆C的切线在x轴和y轴上的截距相等,求此切线的方程.
①当切线在两坐标轴上的截距为零时,设切线方程为y=kx,
则 ![]() ,解得k=2±
,解得k=2± ![]() ,
,
从而切线方程为y=(2± ![]() )x.
)x.
②当切线在两坐标轴上的截距不为零时,设切线方程为x+y-a=0,则 ![]() ,解得a=-1或3,
,解得a=-1或3,
从而切线方程为x+y+1=0或x+y-3=0.
综上,切线方程为(2+ ![]() )x-y=0或(2-
)x-y=0或(2- ![]() )x-y=0或x+y+1=0或x+y-3=0
)x-y=0或x+y+1=0或x+y-3=0
(2)点P在直线l:2x-4y+3=0上,过点P作圆C的切线,切点记为M,求使|PM|最小的点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,过正方形ABCD的中心O作OP⊥平面ABCD,已知正方形的边长为2,OP=2,连接AP、BP、CP、DP,M、N分别是AB、BC的中点,以O为原点,射线OM、ON、OP分别为Ox轴、Oy轴、Oz轴的正方向建立空间直角坐标系.若E、F分别为PA、PB的中点,求A、B、C、D、E、F的坐标.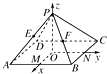
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos(2x ![]() )﹣2sin(x
)﹣2sin(x ![]() )cos(x
)cos(x ![]() )
)
(1)求函数f(x)的最小正周期; (Ⅱ)求函数f(x)在区间[﹣ ![]() ,
, ![]() ]上的值域.
]上的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .
.
(1)求函数f(x)的单调区间和极值;
(2)若函数y=g(x)对任意x满足g(x)=f(4﹣x),求证:当x>2,f(x)>g(x);
(3)若x1≠x2 , 且f(x1)=f(x2),求证:x1+x2>4.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,一个圆锥形的空杯子上放着一个直径为8cm的半球形的冰淇淋,请你设计一种这样的圆锥形杯子(杯口直径等于半球形的冰淇淋的直径,杯子壁厚忽略不计),使冰淇淋融化后不会溢出杯子,怎样设计最省材料?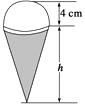
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设 ![]() 是两条不同的直线,
是两条不同的直线, ![]() 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题:
①若 ![]() ,则
,则 ![]() ②若
②若 ![]() ,则
,则 ![]()
③若 ![]() ,则
,则 ![]() ④若
④若 ![]() ,则
,则 ![]()
其中正确命题的序号是( )
A.①和②
B.②和③
C.③和④
D.①和④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com