
【题目】已知数列{an}满a1=a,a2=b,3an+2﹣5an+1+2an=0(n≥0,n∈N),求数列{an}的通项公式.
【答案】解:∵3an+2﹣5an+1+2an=0, ∴an+2﹣an+1= ![]() (an+1﹣an),
(an+1﹣an),
且a2﹣a1=b﹣a.
∴{an+1﹣an}是以b﹣a为首项,以 ![]() 为公比的等比数列,
为公比的等比数列,
∴an+1﹣an=(b﹣a)( ![]() )n﹣1 ,
)n﹣1 ,
∴an﹣an﹣1=(b﹣a)( ![]() )n﹣2 ,
)n﹣2 ,
an﹣1﹣an﹣2=(b﹣a)( ![]() )n﹣3 ,
)n﹣3 ,
…
a3﹣a2=(b﹣a) ![]() ,
,
a2﹣a1=b﹣a,
以上各式相加得:
an﹣a1=(b﹣a)[1+ ![]() +(
+( ![]() )2+…+(
)2+…+( ![]() )n﹣2]=
)n﹣2]= 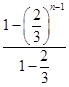 (b﹣a)=3[1﹣(
(b﹣a)=3[1﹣( ![]() )n﹣1](b﹣a).
)n﹣1](b﹣a).
∴an=3[1﹣( ![]() )n﹣1](b﹣a)+a=3b﹣2a+3(
)n﹣1](b﹣a)+a=3b﹣2a+3( ![]() )n﹣1(a﹣b)
)n﹣1(a﹣b)
【解析】将条件式移项可得an+2﹣an+1= ![]() (an+1﹣an),故而{an+1﹣an}是等比数列,从而得出an﹣an﹣1=(b﹣a)(
(an+1﹣an),故而{an+1﹣an}是等比数列,从而得出an﹣an﹣1=(b﹣a)( ![]() )n﹣2 , 使用累加法求出通项公式.
)n﹣2 , 使用累加法求出通项公式.
【考点精析】关于本题考查的数列的通项公式,需要了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】某高校大一新生中的6名同学打算参加学校组织的“演讲团”、“吉他协会”等五个社团,若每名同学必须参加且只能参加1个社团且每个社团至多两人参加,则这6个人中没有人参加“演讲团”的不同参加方法数为( )
A. 3600 B. 1080 C. 1440 D. 2520
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)过点A(2,0),B(0,1)两点.
=1(a>b>0)过点A(2,0),B(0,1)两点.
(1)求椭圆C的方程及离心率;
(2)设直线l与椭圆相交于不同的两点A,B.已知点A的坐标为(﹣a,0),点 Q(0,y0)在线段AB的垂直平分线上,且 ![]()
![]() =4,求y0的值.
=4,求y0的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(π﹣2x),g(x)=2cos2x,则下列结论正确的是( )
A.函数f(x)在区间[ ![]() ]上为增函数
]上为增函数
B.函数y=f(x)+g(x)的最小正周期为2π
C.函数y=f(x)+g(x)的图象关于直线x= ![]() 对称
对称
D.将函数f(x)的图象向右平移 ![]() 个单位,再向上平移1个单位,得到函数g(x)的图象
个单位,再向上平移1个单位,得到函数g(x)的图象
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的几何体中,四边形AA1B1B是边长为3的正方形,CC1=2,CC1∥AA1 , 这个几何体是棱柱吗?若是,指出是几棱柱.若不是棱柱,请你试用一个平面截去一部分,使剩余部分是一个棱长为2的三棱柱,并指出截去的几何体的特征,在立体图中画出截面. 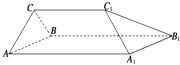
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个透明密闭的正方体容器中,恰好盛有该容器一半容积的水,任意转动这个正方体,则水面在容器中的形状可以是:
①三角形;②矩形;③正方形;④正六边形.
其中正确的结论是(把你认为正确的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB是圆O的直径,C是圆O上不同于A,B的一点,PA⊥平面ABC,E是PC的中点, ![]() ,PA=AC=1.
,PA=AC=1. 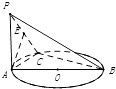
(1)求证:AE⊥PB;
(2)求二面角A﹣PB﹣C的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数y=sin2x的图象向左平移 ![]() 个单位,再向上平移1个单位,所得图象的函数解析式是( )
个单位,再向上平移1个单位,所得图象的函数解析式是( )
A.y=cos2x
B.y=2cos2x
C.![]()
D.y=2sin2x
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com