
【题目】设正数x,y满足log ![]() x+log3y=m(m∈[﹣1,1]),若不等式3ax2﹣18xy+(2a+3)y2≥(x﹣y)2有解,则实数a的取值范围是( )
x+log3y=m(m∈[﹣1,1]),若不等式3ax2﹣18xy+(2a+3)y2≥(x﹣y)2有解,则实数a的取值范围是( )
A.(1, ![]() ]
]
B.(1, ![]() ]
]
C.[ ![]() ,+∞)
,+∞)
D.[ ![]() ,+∞)
,+∞)
【答案】C
【解析】解:∵log ![]() x+log3y=m,即log3
x+log3y=m,即log3 ![]() +log3y=log3
+log3y=log3 ![]() =m, ∴
=m, ∴ ![]() =3m , ∵m∈[﹣1,1],∴
=3m , ∵m∈[﹣1,1],∴ ![]() ∈[
∈[ ![]() ,3].
,3].
∵3ax2﹣18xy+(2a+3)y2≥(x﹣y)2 ,
∴3a﹣18 ![]() +(2a+3)
+(2a+3) ![]() ≥1﹣2
≥1﹣2 ![]() +
+ ![]() ,
,
令 ![]() =t,则2(a+1)t2﹣16t+3a﹣1≥0,
=t,则2(a+1)t2﹣16t+3a﹣1≥0,
设f(t)=2(a+1)t2﹣16t+3a﹣1,
∵不等式3ax2﹣18xy+(2a+3)y2≥(x﹣y)2有解,
∴f(t)在[ ![]() ,3]上的最大值fmax(x)≥0,
,3]上的最大值fmax(x)≥0,
(i)当a=﹣1时,f(t)=﹣16t﹣4,
∴fmax(t)=f( ![]() )=﹣
)=﹣ ![]() ﹣4<0,不符合题意;
﹣4<0,不符合题意;
(ii)若a<﹣1,则f(t)开口向下,对称轴为t= ![]() <0,
<0,
∴f(t)在[ ![]() ,3]上单调递减,
,3]上单调递减,
∴fmax(t)=f( ![]() )=
)= ![]() ﹣6<0,不符合题意;
﹣6<0,不符合题意;
(iii)若a>﹣1,则f(t)开口向上,对称轴为t= ![]() >0,
>0,
①若0< ![]() ≤
≤ ![]() ,即a≥11时,f(t)在[
,即a≥11时,f(t)在[ ![]() ,3]上单调递增,
,3]上单调递增,
∴fmax(t)=f(3)=21a﹣31>0,符合题意;
②若 ![]() ,即﹣1<a
,即﹣1<a ![]() 时,f(t)在[
时,f(t)在[ ![]() ,3]上单调递减,
,3]上单调递减,
∴fmax(t)=f( ![]() )=
)= ![]() ﹣6≤
﹣6≤ ![]() ﹣6<0,不符合题意;
﹣6<0,不符合题意;
③若 ![]() <
< ![]() <3,即
<3,即 ![]() <a<11时,f(t)在[
<a<11时,f(t)在[ ![]() ,3]上先减后增,
,3]上先减后增,
∴fmax(t)=f( ![]() )或fmax(t)=f(3),
)或fmax(t)=f(3),
∴f( ![]() )=
)= ![]() ﹣6≥0或f(3)=21a﹣31>0,
﹣6≥0或f(3)=21a﹣31>0,
解得a≥ ![]() 或a≥
或a≥ ![]() ,又
,又 ![]() <a<11,
<a<11,
∴ ![]() ≤a<11,
≤a<11,
综上,a的取值范围是[ ![]() ,+∞).
,+∞).
故选C.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,AB=8,AD=3,点E,F分别为AB、CD的中点,将四边形AEFD沿EF折到A1EFD1的位置,使∠A1EB=120°,如图2所示,点G、H分别在A1B、D1C上,A1G=D1H= ![]() ,过点G、H的平面α与几何体A1EB﹣D1FC的面相交,交线围成一个正方形.
,过点G、H的平面α与几何体A1EB﹣D1FC的面相交,交线围成一个正方形. 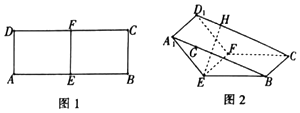
(1)在图中画出这个正方形(不必说明画法和理由);
(2)求点E到平面α的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阅读程序框图,该算法的功能是输出( ) 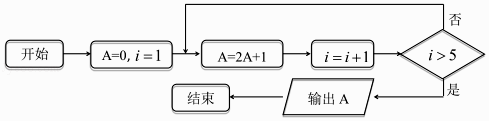
A.数列{2n﹣1}的前 4项的和
B.数列{2n﹣1}的第4项
C.数列{2n}的前5项的和
D.数列{2n﹣1}的第5项
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知非空有限实数集S的所有非空子集依次记为S1 , S2 , S3 , …,集合Sk中所有元素的平均值记为bk . 将所有bk组成数组T:b1 , b2 , b3 , …,数组T中所有数的平均值记为m(T).
(1)若S={1,2},求m(T);
(2)若S={a1 , a2 , …,an}(n∈N* , n≥2),求m(T).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据统计,截至2016年底全国微信注册用户数量已经突破9.27亿,为调查大学生这个微信用户群体中每人拥有微信群的数量,现从某市大学生中随机抽取100位同学进行了抽样调查,结果如下:
微信群数量(个) | 频数 | 频率 |
0~4 | 0.15 | |
5~8 | 40 | 0.4 |
9~12 | 25 | |
13~16 | a | c |
16以上 | 5 | b |
合计 | 100 | 1 |
(Ⅰ)求a,b,c的值及样本中微信群个数超过12的概率;
(Ⅱ)若从这100位同学中随机抽取2人,求这2人中恰有1人微信群个数超过12的概率;
(Ⅲ)以(1)中的频率作为概率,若从全市大学生中随机抽取3人,记X表示抽到的是微信群个数超过12的人数,求X的分布列和数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c分别是△ABC的内角A,B,C所对的边,a=2bcosB,b≠c.
(1)证明:A=2B;
(2)若a2+c2=b2+2acsinC,求A.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 设函数f(x)=emx+x2-mx
设函数f(x)=emx+x2-mx
(1)(I)证明:f(x)在(-![]() ,0)单调递减,在(0,+
,0)单调递减,在(0,+![]() )单调递增;
)单调递增;
(2)(II)若对于任意x1 , x2![]() [-1,1],都有|f(x1)-f(x2)|
[-1,1],都有|f(x1)-f(x2)|![]() e-1,求m的取值范围。
e-1,求m的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com