
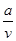 +bv) , 0<v≤c
+bv) , 0<v≤c ≤c时,行驶速度v=
≤c时,行驶速度v= ;当
;当 >c时,行驶速度v=c
>c时,行驶速度v=c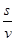 ,全程运输成本为 y=a
,全程运输成本为 y=a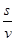 +bv2
+bv2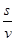 =s(
=s(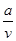 +bv) 故所求函数及定义域为y= s(
+bv) 故所求函数及定义域为y= s(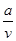 +bv) , 0<v≤c
+bv) , 0<v≤c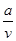 +bv)≥2s
+bv)≥2s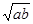 (当且仅当
(当且仅当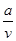 =bv时,即 v=
=bv时,即 v= 时,等号成立)∴v=
时,等号成立)∴v= 时,全程运输成本最小。
时,全程运输成本最小。 ,但速度
,但速度 能否达到呢?没有注意实际问题中的条件限制,使解答不够完整。
能否达到呢?没有注意实际问题中的条件限制,使解答不够完整。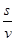 ,全程运输成本为 y=a
,全程运输成本为 y=a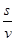 +bv2
+bv2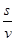 =s(
=s(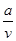 +bv) 故所求函数及定义域为y= s(
+bv) 故所求函数及定义域为y= s(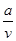 +bv) , 0<v≤c
+bv) , 0<v≤c ≤c,则当v=
≤c,则当v= 时,全程运输成本最小。
时,全程运输成本最小。 >c,当0<v≤c时,易证y是v的增函数,
>c,当0<v≤c时,易证y是v的增函数,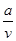 +bv)- s(
+bv)- s(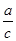 +bc)=s[a(
+bc)=s[a(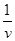 -
-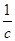 )+b(v-c)]=
)+b(v-c)]= (c-v)(a-bcv)
(c-v)(a-bcv)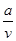 +bv)≥s(
+bv)≥s(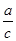 +bc) (当且仅当v=c时,等号成立)
+bc) (当且仅当v=c时,等号成立) ≤c时,行驶速度v=
≤c时,行驶速度v= ;当
;当 >c时,行驶速度v=c。
>c时,行驶速度v=c。

科目:高中数学 来源:不详 题型:单选题
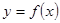 ,其图像是连续不断的,且存在常数
,其图像是连续不断的,且存在常数 (
(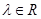 )
)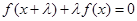 对任意实数
对任意实数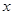 都成立,则称
都成立,则称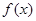 是一个“
是一个“ —伴随函数”. 有
—伴随函数”. 有 —伴随函数”的结论:
—伴随函数”的结论: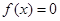 是常数函数中唯一一个“
是常数函数中唯一一个“ —伴随函数”;
—伴随函数”;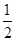 —伴随函数”至少有一个零点;
—伴随函数”至少有一个零点;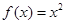 是一个“
是一个“ —伴随函数”;
—伴随函数”;| A.1个; | B.2个; | C.3个; | D.0个; |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
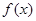 ,若存在区间
,若存在区间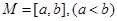 ,使得
,使得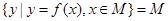 ,则称区间
,则称区间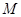 为函数
为函数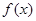 的一个“稳定区间”.现有四个函数:①
的一个“稳定区间”.现有四个函数:①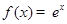 ; ②
; ②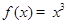 ,
,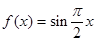 ④
④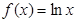 .其中存在“稳定区间”的函数有( )
.其中存在“稳定区间”的函数有( )| A.①② | B.②③ | C.③④ | D.②④ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
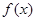 =
=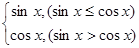 ,给出下列四个命题:①该函数是以
,给出下列四个命题:①该函数是以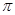 为最小正周期的周期函数;②当且仅当
为最小正周期的周期函数;②当且仅当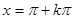 (k∈Z)时,该函数取得最小值-1;
(k∈Z)时,该函数取得最小值-1;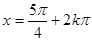 (k∈Z)对称;
(k∈Z)对称;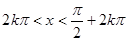 (k∈Z)时,0<
(k∈Z)时,0<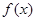 ≤
≤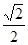 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com