
【题目】某学校运动会的立定跳远和30秒跳绳两个单项比赛分成预赛和决赛两个阶段.下表为10名学生的预赛成绩,其中有三个数据模糊.
学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
立定跳远 (单位:米) | 1.96 | 1.92 | 1.82 | 1.80 | 1.78 | 1.76 | 1.74 | 1.72 | 1.68 | 1.60 |
30秒跳绳 (单位:次) | 63 | a | 75 | 60 | 63 | 72 | 70 | a-1 | b | 65 |
在这10名学生中,进入立定跳远决赛的有8人,同时进入立定跳远决赛和30秒跳绳决赛的有6人,则( )
A. 2号学生进入30秒跳绳决赛 B. 5号学生进入30秒跳绳决赛
C. 8号学生进入30秒跳绳决赛 D. 9号学生进入30秒跳绳决赛
科目:高中数学 来源: 题型:
【题目】某少数民族的刺绣有着悠久的历史,下图![]() 为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含
为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含![]() 个小正方形.
个小正方形.
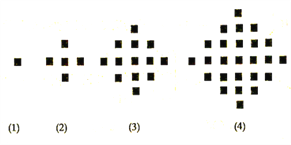
(1)求出![]() ;
;
(2)利用合情推理的“归纳推理思想”归纳出![]() 与
与![]() 的关系式,
的关系式,
(3)根据你得到的关系式求![]() 的表达式
的表达式
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() 为常数,
为常数,![]() ).(Ⅰ)求函数
).(Ⅰ)求函数![]() 的单调区间;(Ⅱ)当
的单调区间;(Ⅱ)当![]() 时,是否存在实数
时,是否存在实数![]() ,使得当
,使得当![]() 时,不等式
时,不等式![]() 恒成立?如果存在,求
恒成立?如果存在,求![]() 的取值范围;如果不存在,请说明理由(其中
的取值范围;如果不存在,请说明理由(其中![]() 是自然对数的底数,
是自然对数的底数,![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】盐化某厂决定采用以下方式对某块盐池进行开采:每天开采的量比上一天减少![]() ,10天后总量变为原来的一半,为了维持生态平衡,剩余总量至少要保留原来的
,10天后总量变为原来的一半,为了维持生态平衡,剩余总量至少要保留原来的![]() ,已知到今天为止,剩余的总量是原来的
,已知到今天为止,剩余的总量是原来的![]() .
.
(1)求![]() 的值;
的值;
(2)到今天为止,工厂已经开采了几天?
(3)今后最多还能再开采多少天?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .现提供
.现提供![]() 的大致图像的8个选项:
的大致图像的8个选项:
(A)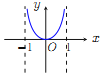 (B)
(B)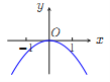 (C)
(C) (D)
(D)
(E) (F)
(F)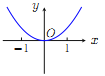 (G)
(G)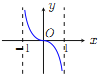 (H)
(H)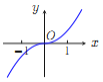
(Ⅰ)请你作出选择,你选的是( );
(Ⅱ)对于函数图像的判断,往往只需了解函数的基本性质.为了验证你的选择的正确性,请你解决下列问题:
①![]() 的定义域是 ;
的定义域是 ;
②就奇偶性而言, ![]() 是 ;
是 ;
③当![]() 时,
时, ![]() 的符号为正还是负?并证明你的结论.
的符号为正还是负?并证明你的结论.
(解决了上述三个问题,你要调整你的选项,还来得及.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的广告费支出x(单位:百万元)与销售额y(单位:百万元)之间有如下的对应数据:
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
(1)画出散点图;
(2)求y关于x的线性回归方程。
(3)如果广告费支出为一千万元,预测销售额大约为多少百万元?
参考公式
用最小二乘法求线性回归方程系数公式: ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】做投掷2个骰子试验,用(x,y)表示点P的坐标,其中x表示第1个骰子出现的点数,y表示第2个骰子出现的点数.
(1)求点P在直线y=x上的概率.
(2)求点P不在直线y=x+1上的概率.
(3)求点P的坐标(x,y)满足16<x2+y2≤25的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知三棱锥P-ABC,∠ACB=90°,CB=4,AB=20,D为AB的中点,且△PDB是正三角形,PA⊥PC.
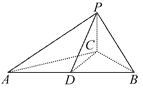
(1)求证:平面PAC⊥平面ABC.
(2)求二面角D-AP-C的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com