
【题目】定义方程f(x)=f′(x)的实数根x0为函数f(x)的“和谐点”.如果函数g(x)=x2(x∈(0,+∞)),h(x)=sin x+2cosx![]() ,φ(x)=ex+x的“和谐点”分别为a,b,c,则a,b,c的大小关系是( )
,φ(x)=ex+x的“和谐点”分别为a,b,c,则a,b,c的大小关系是( )
A. a<b<c B. b<c<a
C. c<b<a D. c<a<b
【答案】D
【解析】
根据题意得到g′(x)=2x,由x2=2x可得x=2,即a=2;h′(x)=cos x-2sin x![]() ,由题意可得sin x+2cos x=cos x-2sin x,
,由题意可得sin x+2cos x=cos x-2sin x,![]() <b<π;φ′(x)=ex+1,可得ex+1=ex+x,解得x=1=c.
<b<π;φ′(x)=ex+1,可得ex+1=ex+x,解得x=1=c.
函数g(x)=x2,x∈(0,+∞),g′(x)=2x,由x2=2x可得x=2,即a=2;函数h(x)=sin x+2cos x,h′(x)=cos x-2sin x![]() ,由题意可得sin x+2cos x=cos x-2sin x,即tan x=-
,由题意可得sin x+2cos x=cos x-2sin x,即tan x=-![]() >-
>-![]() ,∵x∈(0,π),∴
,∵x∈(0,π),∴![]() <x<π,即
<x<π,即![]() <b<π;函数φ(x)=ex+x,由φ′(x)=ex+1,可得ex+1=ex+x,解得x=1,即c=1.综上可知c<a<b.
<b<π;函数φ(x)=ex+x,由φ′(x)=ex+1,可得ex+1=ex+x,解得x=1,即c=1.综上可知c<a<b.
故答案为:D.


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数f(x)满足f(x+2)=2f(x),且当x∈[2,4]时, 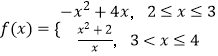 ,g(x)=ax+1,对x1∈[﹣2,0],x2∈[﹣2,1],使得g(x2)=f(x1),则实数a的取值范围为( )
,g(x)=ax+1,对x1∈[﹣2,0],x2∈[﹣2,1],使得g(x2)=f(x1),则实数a的取值范围为( )
A.![]()
B.![]()
C.(0,8]
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an} 为等比数列,等差数列{bn} 的前n 项和为Sn (n∈N* ),且满足:S13=208,S9﹣S7=41,a1=b2 , a3=b3 .
(1)求数列{an},{bn} 的通项公式;
(2)设Tn=a1b1+a2b2+…+anbn (n∈N* ),求Tn;
(3)设cn= ![]() ,问是否存在正整数m,使得cmcm+1cm+2+8=3(cm+cm+1+cm+2).
,问是否存在正整数m,使得cmcm+1cm+2+8=3(cm+cm+1+cm+2).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三年级数学竞赛初赛考试后,对90分以上(含90分)的成绩进行统计,其频率分布直方图如图所示,已知成绩在130~140分数段的人数为2.
(1)求这组数据的平均数M.
(2)现根据初赛成绩从第一组和第五组(从低分段至高分段依次为第一组、第二组、…、第五组)中任意选出两人,形成帮扶小组.若选出的两人的成绩之差大于20,则称这两人为“黄金搭档组”,试求选出的两人为“黄金搭档组”的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数f(x)满足:
(1)函数y=f(x﹣1)的图象关于点(1,0)对称;
(2)对x∈R,f( ![]() ﹣x)=f(
﹣x)=f( ![]() +x)成立
+x)成立
(3)当x∈(﹣ ![]() ,﹣
,﹣ ![]() ]时,f(x)=log2(﹣3x+1),则f(2011)=( )
]时,f(x)=log2(﹣3x+1),则f(2011)=( )
A.﹣5
B.﹣4
C.﹣3
D.﹣2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知各项均不为0的数列{an}满足a1=a,a2=b,且an2=an﹣1an+1+λ(n≥2,n∈N),其中λ∈R.
(1)若λ=0,求证:数列{an}是等比数列;
(2)求证:数列{an}是等差数列的充要条件是λ=(b﹣a)2;
(3)若数列{bn}为各项均为正数的等比数列,且对任意的n∈N* , 满足bn﹣an=1,求证:数列{(﹣1)nanbn}的前2n项和为常数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com