
【题目】设集合S={x|x>1},T={x||x﹣1|≤2},则(RS)∪T( )
A.(﹣∞,3]
B.[﹣1,1]
C.[﹣1,3]
D.[﹣1,+∞)
科目:高中数学 来源: 题型:
【题目】如图1,矩形ABCD中,AB=1,AD=2,点E为AD中点,沿BE将△ABE折起至△PBE,如图2所示,点P在面BCDE的射影O落在BE上. 
(Ⅰ)求证:BP⊥CE;
(Ⅱ)求二面角B﹣PC﹣D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个酒杯的轴截面是一条抛物线的一部分,它的方程是x2=2y,y∈[0,10],在杯内放入一个清洁球,要求清洁球能擦净酒杯的最底部(如图),则清洁球的最大半径为 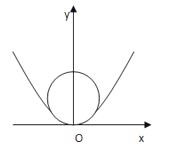
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线m∥平面α,则下列命题中正确的是( )
A.α内所有直线都与直线m异面
B.α内所有直线都与直线m平行
C.α内有且只有一条直线与直线m平行
D.α内有无数条直线与直线m垂直
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,AE⊥平面ABC,CD∥AE,F是BE的中点,AC=BC=1,∠ACB=90°,AE=2CD=2.
证明DF⊥平面ABE;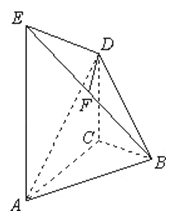
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是首项为15的等比数列,其前n项的和为Sn , 若S3 , S5 , S4成等差数列,则公比q= , 当{an}的前n项的积达到最大时n的值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的首项为a1=1,且 ![]() ,(n∈N*).
,(n∈N*).
(1)求a2 , a3的值,并证明:a2n﹣1<a2n+1<2;
(2)令bn=|a2n﹣1﹣2|,Sn=b1+b2+…+bn . 证明: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义在R上的函数f(x),如果存在实数a,使得f(a+x)f(a﹣x)=1对任意实数x∈R恒成立,则称f(x)为关于a的“倒函数”.已知定义在R上的函数f(x)是关于0和1的“倒函数”,且当x∈[0,1]时,f(x)的取值范围为[1,2],则当x∈[1,2]时,f(x)的取值范围为 , 当x∈[﹣2016,2016]时,f(x)的取值范围为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com