
解:设△ABC的重心P的坐标为(x,y),顶点A的坐标为(x1,y1),则y1=x12-4.
由重心坐标公式得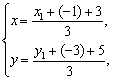
∴![]() 代入y1=x12-4得3y-2=(3x-2)2-4,化简整理得y=3x2-4x+
代入y1=x12-4得3y-2=(3x-2)2-4,化简整理得y=3x2-4x+![]() .
.
又直线BC的方程为![]() =
=![]() ,即y=2x-1,
,即y=2x-1,
由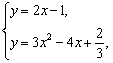
得![]() 或
或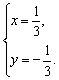
而A、B、C三点不在同一直线上,
∴P、B、C三点不共线,
即轨迹中应去掉点(![]() ,
,![]() )和(
)和(![]() ,-
,-![]() ).
).
故△ABC的重心P的轨迹为开口向上的抛物线y=3x2-4x+![]() ,但不包括点(
,但不包括点(![]() ,
,![]() )和(
)和(![]() ,-
,-![]() ).
).
点评:(1)动点P与A有关系,用P的坐标表示A的坐标,并代入A的轨迹方程得到P的轨迹方程.这种求方程的方法称作相关点法.
(2)求动点的轨迹与求轨迹方程的要求不同,前者是求轨迹图形.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| 12 |
| y2 |
| 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| 3 |
| 3 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com