分析:(I)由直三棱柱的性质,可得AA1⊥BC,由AD⊥平面A1BC,得AD⊥BC,结合线面垂直的判定定理,可得BC⊥平面ABB1A1.
(II)由(I)得BC⊥AB,结合已知条件得△ABC是斜边AC=2的等腰直角三角形,然后在Rt△AA1B中,算出斜边上的高AD的长,根据射影定理算出BD的长,从而得到三角形BCD的面积,最后用锥体体积公式,可以算出三棱锥A-BCD的体积,即得三棱锥A-BCD的体积.
解答:证明:(Ⅰ)∵AD⊥平面A
1BC,BC⊆平面A
1BC,∴AD⊥BC.
∵ABC-A
1B
1C
1是直三棱柱,
∴AA
1⊥平面ABC,可得AA
1⊥BC.…(3分)
∵AD∩AA
1=A,AD、AA
1⊆平面ABB
1A
1,
∴BC⊥平面ABB
1A
1.…(6分)
(Ⅱ)∵BC⊥平面ABB
1A
1,∴BC⊥AB.
∵AB=BC,∴△ABC是等腰直角三角形,且斜边AC=2,AB=BC=
,
∴直角三角形AA
1B斜边上的高
AD===,
根据射影定理,得
BD===∴三棱锥A-BCD的体积V
A-BCD=V
B-ACD=
S
△ACD×BD=
×
•AD•DC•BD=
…(12分)
点评:本题给出特殊的三棱柱,求证线面垂直并且求三棱锥的体积,着重考查了直线与平面垂直的判定与性质和锥体体积公式等知识,属于基础题.

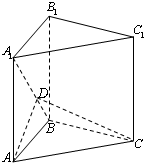 (2012•咸阳三模)如图直三棱柱ABC-A1B1C1中,AC=CC1=2,AB=BC,D是BA1上一点,且AD⊥平面A1BC.
(2012•咸阳三模)如图直三棱柱ABC-A1B1C1中,AC=CC1=2,AB=BC,D是BA1上一点,且AD⊥平面A1BC.

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案