
【题目】已知实数a、m满足a= ![]() cosxdx,(x+a+m)7=a0+a1(x+1)+a2(x+1)2+…+a7(x+1)7 , 且(a0+a2+a4+a6)2﹣(a1+a3+a5+a7)2=37 , 则m=( )
cosxdx,(x+a+m)7=a0+a1(x+1)+a2(x+1)2+…+a7(x+1)7 , 且(a0+a2+a4+a6)2﹣(a1+a3+a5+a7)2=37 , 则m=( )
A.﹣1或3
B.1或﹣3
C.1
D.3
科目:高中数学 来源: 题型:
【题目】已知a>0且满足不等式22a+1>25a﹣2.
(1)求实数a的取值范围;
(2)求不等式loga(3x+1)<loga(7﹣5x);
(3)若函数y=loga(2x﹣1)在区间[1,3]有最小值为﹣2,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线![]() (
(![]() )的焦点为
)的焦点为![]() ,已知点
,已知点![]() ,
, ![]() 为抛物线上的两个动点,且满足
为抛物线上的两个动点,且满足![]() .过弦
.过弦![]() 的中点
的中点![]() 作抛物线准线的垂线
作抛物线准线的垂线![]() ,垂足为
,垂足为![]() ,则
,则![]() 的最大值为__________.
的最大值为__________.
【答案】1
【解析】设![]() ,在三角形ABF中,用余弦定理得到
,在三角形ABF中,用余弦定理得到![]()
![]() ,
, 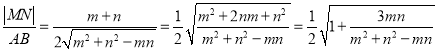
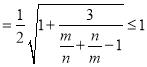 故最大值为1.
故最大值为1.
故答案为:1.
点睛:本题主要考查了抛物线的简单性质.解题的关键是利用了抛物线的定义。一般和抛物线有关的小题,很多时可以应用结论来处理的;平时练习时应多注意抛物线的结论的总结和应用。尤其和焦半径联系的题目,一般都和定义有关,实现点点距和点线距的转化。
【题型】填空题
【结束】
17
【题目】设![]() 的内角
的内角![]() ,
, ![]() ,
, ![]() 所对的边分别为
所对的边分别为![]() ,
, ![]() ,
, ![]() ,且
,且![]() ,
, ![]() .
.
(1)当![]() 时,求
时,求![]() 的值;
的值;
(2)当![]() 的面积为
的面积为![]() 时,求
时,求![]() 的周长.
的周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,过点A作⊙O的切线EP交CB的延长线于P,∠PAB=35°. 
(1)若BC是⊙O的直径,求∠D的大小;
(2)若∠PAB=35°,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() ,半径为2的圆
,半径为2的圆![]() 与
与![]() 相切,圆心
相切,圆心![]() 在
在![]() 轴上且在直线
轴上且在直线![]() 的上方.
的上方.
(1)求圆![]() 的方程;
的方程;
(2)过点![]() 的直线与圆
的直线与圆![]() 交于
交于![]() 两点(
两点(![]() 在
在![]() 轴上方),问在
轴上方),问在![]() 轴正半轴上是否存在定点
轴正半轴上是否存在定点![]() ,使得
,使得![]() 轴平分
轴平分![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为奇函数,
为奇函数,![]() 为偶函数,且
为偶函数,且![]() .
.
(Ⅰ)求函数![]() 及
及![]() 的解析式;
的解析式;
(Ⅱ)用函数单调性的定义证明:函数![]() 在
在![]() 上是减函数;
上是减函数;
(Ⅲ)若关于![]() 的方程
的方程![]() 有解,求实数
有解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.
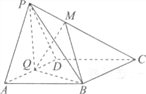
(Ⅰ)若PA=PD,求证:平面PQB⊥平面PAD;
(Ⅱ)点M在线段PC上,PM=tPC,试确定实数t的值,使PA∥平面MQB;
(Ⅲ)在(Ⅱ)的条件下,若平面PAD⊥平面ABCD,且PA=PD=AD=2,求二面角M-BQ-C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设双曲线C的中心为点O,若有且只有一对相交于点O,所成的角为60°的直线A1B1和A2B2,使| A1B1|=| A2B2|,其中A1,B1和A2,B2分别是这对直线与双曲线C的交点,则该双曲线的离心率的取值范围是( )
A. (![]() ,2] B. [
,2] B. [![]() ,2) C. (
,2) C. (![]() ,+
,+![]() ) D. [
) D. [![]() ,+
,+![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com