
【题目】中国改革开放以来经济发展迅猛,某一线城市的城镇居民2012~2018年人均可支配月收入散点图如下(年份均用末位数字减1表示).
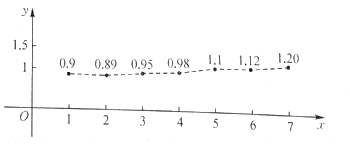
(1)由散点图可知,人均可支配月收入y(万元)与年份x之间具有较强的线性相关关系,试求y关于x的回归方程(系数精确到0.001),依此相关关系预测2019年该城市人均可支配月收入;
(2)在2014~2018年的五个年份中随机抽取两个数据作样本分析,求所取的两个数据中,人均可支配月收入恰好有一个超过1万元的概率.
注: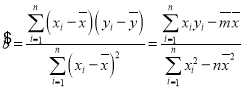 ,
,![]() ,
,![]() ,
,![]()
科目:高中数学 来源: 题型:
【题目】设等差数列{an}的前n项和为Sn,已知:a5=2a2+3且a2,![]() ,a14成等比数列.
,a14成等比数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设正项数列{bn}满足bn2Sn+1=Sn+1+2,求证:b1+b2+…+bn<n+1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某医院体检中心为回馈大众,推出优惠活动:对首次参加体检的人员,按200元/次收费,并注册成为会员,对会员的后续体检给予相应优惠(本次即第一次),标准如下:
体检次序 | 第一次 | 第二次 | 第三次 | 第四次 | 第五次及以上 |
收费比例 | 1 | 0.95 | 0.90 | 0.85 | 0.8 |
该体检中心从所有会员中随机选取了100位对他们在本中心参加体检的次数进行统计,得到数据如下表:
体检次数 | 一次 | 两次 | 三次 | 四次 | 五次及以上 |
频数 | 60 | 20 | 12 | 4 | 4 |
假设该体检中心为顾客体检一次的成本费用为150元,根据所给数据,解答下列问题:
(1)已知某顾客在此体检中心参加了3次体检,求这3次体检,该体检中心的平均利润;
(2)该体检中心要从这100人里至少体检3次的会员中,按体检次数用分层抽样的方法抽出5人,再从这5人中抽取2人发放纪念品,求抽到的2人中恰有1人体检3次的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双曲线定位法是通过测定待定点到至少三个已知点的两个距离差所进行的一种无线电定位.通过船(待定点)接收到三个发射台的电磁波的时间差计算出距离差,两个距离差即可形成两条位置双曲线,两者相交便可确定船位.我们来看一种简单的“特殊”状况;如图所示,已知三个发射台分别为![]() ,
,![]() ,
,![]() 且刚好三点共线,已知
且刚好三点共线,已知![]() 海里,
海里,![]() 海里,现以
海里,现以![]() 的中点为原点,
的中点为原点,![]() 所在直线为
所在直线为![]() 轴建系.现根据船
轴建系.现根据船![]() 接收到
接收到![]() 点与
点与![]() 点发出的电磁波的时间差计算出距离差,得知船
点发出的电磁波的时间差计算出距离差,得知船![]() 在双曲线
在双曲线![]() 的左支上,若船
的左支上,若船![]() 上接到
上接到![]() 台发射的电磁波比
台发射的电磁波比![]() 台电磁波早
台电磁波早![]() (已知电磁波在空气中的传播速度约为
(已知电磁波在空气中的传播速度约为![]() ,1海里
,1海里![]() ),则点
),则点![]() 的坐标(单位:海里)为( )
的坐标(单位:海里)为( )
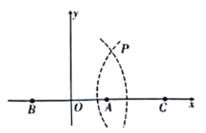
A. B.
B.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴长为4,且经过点
的长轴长为4,且经过点 .
.
(1)求椭圆的方程;
(2)直线![]() 的斜率为
的斜率为![]() ,且与椭圆相交于
,且与椭圆相交于![]() ,
,![]() 两点(异于点
两点(异于点![]() ),过
),过![]() 作
作![]() 的角平分线交椭圆于另一点
的角平分线交椭圆于另一点![]() .证明:直线
.证明:直线![]() 与坐标轴平行.
与坐标轴平行.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂预购软件服务,有如下两种方案:
方案一:软件服务公司每日收取工厂60元,对于提供的软件服务每次10元;
方案二:软件服务公司每日收取工厂200元,若每日软件服务不超过15次,不另外收费,若超过15次,超过部分的软件服务每次收费标准为20元.
(1)设日收费为![]() 元,每天软件服务的次数为
元,每天软件服务的次数为![]() ,试写出两种方案中
,试写出两种方案中![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)该工厂对过去100天的软件服务的次数进行了统计,得到如图所示的条形图,依据该统计数据,把频率视为概率,从节约成本的角度考虑,从两个方案中选择一个,哪个方案更合适?请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() 的离心率为
的离心率为![]() ,以椭圆
,以椭圆![]() 的上顶点
的上顶点![]() 为圆心作圆,
为圆心作圆,
![]() ,圆
,圆![]() 与椭圆
与椭圆![]() 在第一象限交于点
在第一象限交于点![]() ,在第二象限交于点
,在第二象限交于点![]() .
.
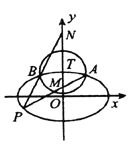
(1)求椭圆![]() 的方程;
的方程;
(2)求![]() 的最小值,并求出此时圆
的最小值,并求出此时圆![]() 的方程;
的方程;
(3)设点![]() 是椭圆
是椭圆![]() 上异于
上异于![]() 的一点,且直线
的一点,且直线![]() 分别与
分别与![]() 轴交于点
轴交于点![]() 为坐标原点,求证:
为坐标原点,求证:
![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com