
分析 化简可得2(x+y)2+x2y2≤9,从而令x+y=w,xy=v,从而得到2w2+v2≤9,u=2$\sqrt{2}$w+v,w=-$\frac{v}{2\sqrt{2}}$+$\frac{u}{2\sqrt{2}}$,从而利用数形结合的思想求解即可.
解答 解:∵2x2+4xy+2y2+x2y2≤9,
∴2(x+y)2+x2y2≤9,
令x+y=w,xy=v,
则2w2+v2≤9,
即$\frac{{w}^{2}}{4.5}$+$\frac{{v}^{2}}{9}$≤1,
u=2$\sqrt{2}$(x+y)+xy=2$\sqrt{2}$w+v,
∴w=-$\frac{v}{2\sqrt{2}}$+$\frac{u}{2\sqrt{2}}$,
作图如下, ,
,
由$\left\{\begin{array}{l}{2{w}^{2}+{v}^{2}=9}\\{w=-\frac{\sqrt{2}}{4}v+\frac{\sqrt{2}}{4}u}\end{array}\right.$有且只有一个解知,
即5v2-2uv+u2-36=0只有一个解,
故△=4u2-4×5×(u2-36)=0,
从而解得,u=3$\sqrt{5}$或u=-3$\sqrt{5}$;
故u=2$\sqrt{2}$(x+y)+xy的最大值为3$\sqrt{5}$,最小值为-3$\sqrt{5}$.
点评 本题考查了圆锥曲线的应用及数形结合的思想应用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{6}$个单位长度 | B. | 向右平移$\frac{π}{6}$个单位长度 | ||
| C. | 向左平移$\frac{π}{3}$个单位长度 | D. | 向右平移$\frac{π}{3}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
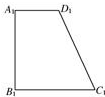 如图,已知四边形ABCD的直观图是直角梯形A1B1C1D1,且A1B1=B1C1=2A1D1=4,则四边形ABCD的面积为( )
如图,已知四边形ABCD的直观图是直角梯形A1B1C1D1,且A1B1=B1C1=2A1D1=4,则四边形ABCD的面积为( )| A. | 12 | B. | 12$\sqrt{2}$ | C. | 24$\sqrt{2}$ | D. | 24 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f($\frac{π}{3}$)>$\sqrt{2}$f($\frac{π}{4}$) | B. | f($\frac{π}{3}$)>2cos1•f(1) | C. | 2cos1•f(1)>$\sqrt{2}$f($\frac{π}{4}$) | D. | $\sqrt{2}$f($\frac{π}{4}$)<$\sqrt{3}$f($\frac{π}{6}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com