
【题目】已知函数fk(x)=2x﹣(k﹣1)2﹣x(k∈Z),x∈R,g(x)= ![]() .
.
(1)若f2(x)=2,求x的值.
(2)判断并证明函数y=g(x)的单调性;
(3)若函数y=f0(2x)+2mf2(x)在x∈[1,+∞)上有零点,求实数m的取值范围.
【答案】
(1)解:由题意得: ![]()
由题意, ![]() ∴
∴ ![]() ,
,
∴(2x)2﹣2(2x)﹣1=0
∴ ![]() ,或
,或 ![]() (舍去)∴
(舍去)∴ ![]()
(2)解: ![]() ,
,
∵当x变大时,4x+1变大, ![]() 也变大,g(x)变大
也变大,g(x)变大
∴g(x)在R上单调递增.
证明:任取x1,x2∈R,且x1<x2
则f(x1)﹣f(x2)= ![]() =
= ![]()
= ![]() =
= ![]()
∴x1<x2
∴ ![]()
∴ ![]() ,
, ![]()
∴f(x1)﹣f(x2)<0
∴f(x1)<f(x2)
∴f(x)在R上是增函数
(3)解:y=f0(2x)+2mf2(x)=22x+2﹣2x+2m(2x﹣2﹣x)=(2x﹣2﹣x)2+2+2m(2x﹣2﹣x)
令t=2x﹣2﹣x,则t在R上单调递增.
∵x∈[1,+∞),∴ ![]()
条件等价于 ![]() 在x∈[1,+∞)上有零点,
在x∈[1,+∞)上有零点,
即: ![]() 在
在 ![]() 上有零点
上有零点
令 ![]() 任取
任取 ![]() ,
,
则 ![]()
∵ ![]() ∴
∴ ![]() ∴h(t1)﹣h(t2)<0∴h(t1)<h(t2)
∴h(t1)﹣h(t2)<0∴h(t1)<h(t2)
∴h(t)在 ![]() 上单调递增
上单调递增
∴当 ![]() 时,
时, ![]() ,即
,即 ![]()
所以, ![]()
【解析】1、由代入特殊值可得 f2 ( x ) = 2 x 2 x = 2 ∴ 2 x 1 2 x = 2 ,∴(2x)2﹣2(2x)﹣1=0,由指对互化可得结果。
2、由函数的增减性定义可得该函数为增函数。
3、整体思想代换令t=2x﹣2﹣x, t ≥ ![]() 即 2 m =
即 2 m = ![]() = t +
= t +![]() 在 t ≥
在 t ≥![]() 上有零点,.令 h ( t ) = t +
上有零点,.令 h ( t ) = t + ![]() , t ∈ [
, t ∈ [ ![]() , + ∞ ) 任取 3 2 ≤ t1 < t2 ,则 h ( t1 ) h ( t2 ) =
, + ∞ ) 任取 3 2 ≤ t1 < t2 ,则 h ( t1 ) h ( t2 ) =![]() ,由增减函数的定义可得h(t)在 [
,由增减函数的定义可得h(t)在 [ ![]() , + ∞ ) 上单调递增,所以, m ≤
, + ∞ ) 上单调递增,所以, m ≤ ![]()
【考点精析】关于本题考查的函数单调性的判断方法,需要了解单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较才能得出正确答案.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:高中数学 来源: 题型:
【题目】人们生活水平的提高,越来越注重科学饮食.营养学家指出,成人良好的日常饮食应该至少提供0.075kg的碳水化合物,0.06kg的蛋白质,0.06kg的脂肪.1kg食物A含有0.105kg碳水化合物,0.07kg蛋白质,0.14kg脂肪,花费28元;而1kg食物B含有0.105kg碳水化合物,0.14kg蛋白质,0.07kg脂肪,花费21元.为了满足营养专家指出的日常饮食要求,同时使花费最低,每天需要同时食用食物A和食物B多少kg?最低花费是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为(0,+∞)的函数f(x)满足:
①x>1时,f(x)<0;
②f( ![]() )=1;
)=1;
③对任意的正实数x,y,都有f(xy)=f(x)+f(y).
(1)求证:f( ![]() )=﹣f(x);
)=﹣f(x);
(2)求证:f(x)在定义域内为减函数;
(3)求满足不等式f(log0.5m+3)+f(2log0.5m﹣1)≥﹣2的m集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在原点的双曲线C的右焦点为(2,0),右顶点为( ![]() ,0)
,0)
(1)求双曲线C的方程;
(2)若直线l:y=kx+ ![]() 与双曲线C恒有两个不同的交点A和B,且
与双曲线C恒有两个不同的交点A和B,且 ![]() >2(其中O为原点).求k的取值范围.
>2(其中O为原点).求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥A﹣BCDE中,底面BCDE为平行四边形,平面ABE⊥平面BCDE,AB=AE,DB=DE,∠BAE=∠BDE=90°
(1)求异面直线AB与DE所成角的大小;
(2)求二面角B﹣AE﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:函数f(x)=logax在区间(0,+∞)上是单调递增函数;命题q:不等式(a﹣2)x2+2(a﹣2)x﹣4<0对任意实数x恒成立.若p∨q为真命题,且p∧q为假命题,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|lgx|﹣( ![]() )x有两个零点x1 , x2 , 则有( )
)x有两个零点x1 , x2 , 则有( )
A.x1x2<0
B.x1x2=1
C.x1x2>1
D.0<x1x2<1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx+2x+x﹣1,若f(x2﹣4)<2,则实数x的取值范围是( )
A.(﹣2,2)
B.(2, ![]() )
)
C.(﹣ ![]() ,﹣2)
,﹣2)
D.(﹣ ![]() ,﹣2)∪(2,
,﹣2)∪(2, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱 ![]() 中,底面
中,底面 ![]() 是边长为2的等边三角形,
是边长为2的等边三角形, ![]() 为
为 ![]() 的中点.
的中点.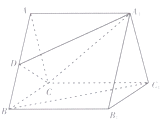
(1)求证: ![]() 平面
平面 ![]() ;
;
(2)若四边形 ![]() 是正方形,且
是正方形,且 ![]() , 求直线
, 求直线 ![]() 与平面
与平面 ![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com