
���� ��1���������Ǻ�ʽ�Ե�ʽ���л������������$\frac{sinAcosB}{cosAsinB}$=$\frac{{a}^{2}}{{b}^{2}}$���������Ҷ���ת���ɽǵ����ң�����Լ�����sin2A=sin2B������ȷ��A��B�Ĺ�ϵ��ȷ�������ε���״��
��2���������Ҷ�������֪��ʽ�еı߾���Ϊ�ǵ����Ǻ���ʽ����Ӧ�����Ǻ͵����ҹ�ʽ��֤cos��B+C��=0��ʹ����ý⣺
��3���������Ҷ�����������ǺͲ�����ҹ�ʽ�����ҹ�ʽ���л������������ε������ʽ�Լ����Ҷ�����ϻ�������ʽ������⼴�ɣ�
��4���������ǺͲ�����й�ʽ������Ҷ����Լ����ǺͲ�����ҹ�ʽ���л����ǽ������Ĺؼ���
��� �⣺�߶��ڣ�1������a2-b2��sin��A+B��=��a2+b2��sin��A-B����
�ࣨa2-b2����sinAcosB+cosAsinB��=��a2+b2����sinAcosB-cosAsinB����
�������a2cosAsinB=b2sinAcosB��
����$\frac{sinAcosB}{cosAsinB}$=$\frac{{a}^{2}}{{b}^{2}}$=$\frac{si{n}^{2}A}{si{n}^{2}B}$��
��sinAcosA=sinBcosB��
��sin2A=sin2B��
��A=B��A+B=$\frac{��}{2}$
���ABC�ǵ�������Rt����
���ڣ�2���������Ҷ�����ԭʽ��Ϊ��
8k2sin2Bsin2C=8k2sinBsinCcosBcosC��
��sinBsinC��0��
��sinBsinC=cosBcosC��
��cos��B+C��=0��
��B+C=90�㣬A=90�㣬
�ʡ�ABCΪֱ�������Σ�
���ڣ�3������ $\frac{cosB}{cosC}$=-$\frac{b}{2a+c}$�ã�$\frac{cosB}{cosC}$=-$\frac{sinB}{2sinA+sinC}$��
��2sinAcosB+cosBsinC+sinBcosC=0��
��2sinAcosB+sin��B+C��=2sinAcosB+sinA=0����sinA��2cosB+1��=0��
��0��A������sinA��0����cosB=-$\frac{1}{2}$��
��b=$\sqrt{13}$��
�������Ҷ���b2=a2+c2-2accosB��
��13=a2+c2+ac��3ac����ac��$\frac{13}{3}$��
��S��ABC=$\frac{1}{2}$acsinB��$\frac{1}{2}$��$\frac{13}{3}$��$\frac{\sqrt{3}}{2}$=$\frac{13\sqrt{3}}{12}$�����ҽ���acʱȡ�Ⱥţ���
���ABC������ֵΪ$\frac{13\sqrt{3}}{12}$��
���ڣ�4������$\sqrt{3}$tanA•tanB-tanA-tanB=$\sqrt{3}$��
��$\frac{tanA+tanB}{1-tanAtanB}$=-$\sqrt{3}$����tan��A+B��=-tanC=-$\sqrt{3}$��
��tanC=$\sqrt{3}$��
�ߡ�CΪ�����ε��ڽǣ�
���C=$\frac{��}{3}$��
�ߡ�A���BΪ��ǣ��ҡ�A+��B=��-��C=$\frac{2��}{3}$������B=$\frac{2��}{3}$-��A��
��$\frac{��}{6}$����A��$\frac{��}{2}$��
��$\frac{��}{6}$��2��A-$\frac{��}{6}$��$\frac{5��}{6}$��
��c=2��sinC=$\frac{\sqrt{3}}{2}$��
�������Ҷ���$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$=$\frac{2}{\frac{\sqrt{3}}{2}}$�ã�a=$\frac{4\sqrt{3}}{3}$sinA��b=$\frac{4\sqrt{3}}{3}$sinB��
��a2+b2=$\frac{16}{3}$��sinA+sinB��=$\frac{16}{3}$[sinA+sin��$\frac{2��}{3}$-A��]=$\frac{16}{3}$+$\frac{8}{3}$sin��2A-$\frac{��}{6}$����
��$\frac{��}{6}$��2��A-$\frac{��}{6}$��$\frac{5��}{6}$��
��$\frac{1}{2}$��sin��2A-$\frac{��}{6}$����1����$\frac{20}{3}$��$\frac{16}{3}$+$\frac{8}{3}$sin��2A-$\frac{��}{6}$����8��
��a2+b2�ķ�ΧΪ��$\frac{20}{3}$��8]��
���� ���⿼��������ε�Ӧ�ã��������Ǻ��������Һ�����ʽ�����Ҷ��������Ҷ������Լ����Ǻ��������к�����ʽ���������չ�ʽ�������ǽⱾ��Ĺؼ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�$\frac{1}{2}$�� | B�� | [1��$\frac{3}{2}$]�ȣ�$\frac{7}{4}$��2] | C�� | ��-�ޣ�$\frac{1}{2}$����[1��2] | D�� | ��$\frac{3}{2}$��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | $\sqrt{3}$ | C�� | 2 | D�� | 2$\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
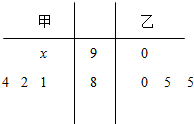 ��ͼ�þ�Ҷͼ��¼��ͬ��ļס�������ѧ��4����ѧ���Գɼ������м�һ�γɼ�ģ�����壬��x��ǣ�
��ͼ�þ�Ҷͼ��¼��ͬ��ļס�������ѧ��4����ѧ���Գɼ������м�һ�γɼ�ģ�����壬��x��ǣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {x|1��x��2} | B�� | {x|1��x��2} | C�� | {x|2��x��3} | D�� | {x|2��x��3} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com