
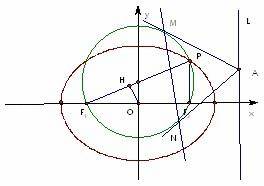
已知椭圆![]() 左右两焦点为F1,F2,P是椭圆上一点,且在x轴上方,PF2⊥F1F2,OH⊥PF1于H,
左右两焦点为F1,F2,P是椭圆上一点,且在x轴上方,PF2⊥F1F2,OH⊥PF1于H,![]() .
.
(1)求椭圆的离心率e的取值范围;
(2)当e取最大值时,过F1,F2,P的圆Q的截y轴的线段长为6,求圆Q的方程;
(3)在(2)的条件下,过椭圆右准线L上任一点A引圆Q的两条切线,切点分别为M,N,试探究直线MN是否过定点?若过定点,请求出该定点;否则,请说明理由.
考点:
圆与圆锥曲线的综合.
专题:
综合题.
分析:
由相似三角形知,![]() ,
,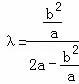 ,2a2λ﹣b2λ=b2,2a2λ=b2(1+λ),
,2a2λ﹣b2λ=b2,2a2λ=b2(1+λ),![]() .
.
(1)由![]() ,知
,知![]() ,在
,在![]() 上单调递减.由此能求出椭圆的离心率e的取值范围.
上单调递减.由此能求出椭圆的离心率e的取值范围.
(2)当![]() 时,
时,![]() ,所以
,所以![]() ,2b2=a2.由PF2⊥F1F2,知PF1是圆的直径,圆心是PF1的中点,由此能求出圆Q的方程.
,2b2=a2.由PF2⊥F1F2,知PF1是圆的直径,圆心是PF1的中点,由此能求出圆Q的方程.
(3)椭圆方程是![]() ,右准线方程为
,右准线方程为![]() ,由直线AM,AN是圆Q的两条切线,知切点M,N在以AQ为直径的圆上.设A点坐标为
,由直线AM,AN是圆Q的两条切线,知切点M,N在以AQ为直径的圆上.设A点坐标为![]() ,由此能够导出直线MN必过定点
,由此能够导出直线MN必过定点![]() .
.
解答:
解:由相似三角形知,![]() ,
,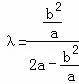 ,
,
∴2a2λ﹣b2λ=b2,2a2λ=b2(1+λ),![]() .
.
(1)![]() ,∴
,∴![]() ,在
,在![]() 上单调递减.
上单调递减.
∴![]() 时,e2最小
时,e2最小![]() ,
,![]() 时,e2最大
时,e2最大![]() ,
,
∴![]() ,∴
,∴![]() .
.
(2)当![]() 时,
时,![]() ,∴
,∴![]() ,∴2b2=a2.
,∴2b2=a2.
∵PF2⊥F1F2,∴PF1是圆的直径,圆心是PF1的中点,
∴在y轴上截得的弦长就是直径,∴PF1=6.
又![]() ,∴
,∴![]() .
.
∴![]() ,圆心Q(0,1),半径为3,x2+(y﹣1)2=9.
,圆心Q(0,1),半径为3,x2+(y﹣1)2=9.
(3)椭圆方程是![]() ,右准线方程为
,右准线方程为![]() ,
,
∵直线AM,AN是圆Q的两条切线,∴切点M,N在以AQ为直径的圆上.设A点坐标为![]() ,
,
∴该圆方程为![]() .∴直线MN是两圆的公共弦,两圆方程相减得:
.∴直线MN是两圆的公共弦,两圆方程相减得:![]() ,这就是直线MN的方程.
,这就是直线MN的方程.
该直线化为:![]() ,
,
∴![]() ,∴
,∴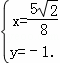
∴直线MN必过定点![]() .
.
点评:
本题考查直线 和圆锥曲线的位置关系的综合运用,解题时要认真审题,注意挖掘题设中的隐含条件.


科目:高中数学 来源:2012-2013学年江苏省扬州中学高二(上)期末数学试卷(解析版) 题型:解答题
 左右两焦点为F1,F2,P是椭圆上一点,且在x轴上方,PF2⊥F1F2,OH⊥PF1于H,
左右两焦点为F1,F2,P是椭圆上一点,且在x轴上方,PF2⊥F1F2,OH⊥PF1于H, .
.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北省宜昌市长阳一中高二(下)第一次月考数学试卷(理科)(解析版) 题型:解答题
 左右两焦点为F1,F2,P是椭圆上一点,且在x轴上方,PF2⊥F1F2,OH⊥PF1于H,
左右两焦点为F1,F2,P是椭圆上一点,且在x轴上方,PF2⊥F1F2,OH⊥PF1于H,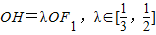 .
.
查看答案和解析>>
科目:高中数学 来源:2011年江苏省高考数学预测试卷(3)(解析版) 题型:解答题
 左右两焦点为F1,F2,P是椭圆上一点,且在x轴上方,PF2⊥F1F2,OH⊥PF1于H,
左右两焦点为F1,F2,P是椭圆上一点,且在x轴上方,PF2⊥F1F2,OH⊥PF1于H, .
.
查看答案和解析>>
科目:高中数学 来源:2011年江苏高考数学预测试卷(解析版) 题型:解答题
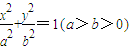 左右两焦点为F1,F2,P是椭圆上一点,且在x轴上方,PF2⊥F1F2,OH⊥PF1于H,
左右两焦点为F1,F2,P是椭圆上一点,且在x轴上方,PF2⊥F1F2,OH⊥PF1于H,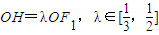 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com