己知二次函数y=f(x) 的图象过点(1,-4),且不等式f(x)<0的解集是(O,5).
(I )求函数f(x)的解析式;
(II)设g(x)=x3-(4k-10)x+5,若函数h(x)=2f(x)+g(x)在[-4,-2]上单调递增,在[-2,0]上单调递减,求y=h(x)在[-3,1]上的最大值和最小值..
【答案】
分析:(1)根据函数零点,方程根与不等式解集端点之间的关系,结合二次函数y=f(x) 的图象过点(1,-4),可求出函数f(x)的解析式;
(II)由(I)可求出函数h(x)的解析式(含参数k),进而由函数极大值点为-2,求出k值,结合导数法求最值的步骤,可得答案.
解答:解:(Ⅰ)由已知y=f (x)是二次函数,且f (x)<0的解集是(0,5),
可得f (x)=0的两根为0,5,
于是设二次函数f (x)=ax(x-5),
代入点(1,-4),得-4=a×1×(1-5),解得a=1,
∴f (x)=x(x-5). …(4分)
(Ⅱ)h(x)=2f (x)+g(x)=2x(x-5)+x
3-(4k-10)x+5=x
3+2x
2-4kx+5,
于是h′(x)=3x
2+4x-4k,
∵h(x)在[-4,-2]上单调递增,在[-2,0]上单调递减,
∴x=-2是h(x)的极大值点,
∴h′(2)=3×(-2)
2+4×(-2)-4k=0,解得k=1. …(6分)
∴h(x)=x
3+2x
2-4x+5,进而得h′(x)=3x
2+4x-4.
令h′(x)=3x
2+4x-4=0,得x=-2,或x=

.
由下表:
| x | (-3,-2) | -2 | (-2, ) ) |  | ( ,1) ,1) |
| h′(x) | + | | - | | + |
| h(x) | ↗ | 极大 | ↘ | 极小 | ↗ |
可知:h(-2)=(-2)
3+2×(-2)
2-4×(-2)+5=13,h(1)=1
3+2×1
2-4×1+5=4,
h(-3)=(-3)
3+2×(-3)
2-4×(-3)+5=8,h(

)=(

)
3+2×(

)
2-4×

+5=
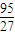
,
∴h(x)的最大值为13,最小值为
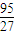
.…(12分)
点评:本题考查的知识点是二次函数的性质,函数零点,方程根与不等式解集端点的关系,导数法求函数的极值与最值,其中求出函数h(x)的解析式是解答的关键.

 .
. )
)
 ,1)
,1) )=(
)=( )3+2×(
)3+2×( )2-4×
)2-4× +5=
+5=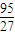 ,
,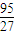 .…(12分)
.…(12分)
