
【题目】设l,m是两条不同直线,α是一个平面,则下列四个命题正确的是( )
A.若l⊥m,mα,则l⊥α
B.若l∥α,m∥α,则l∥m
C.若l∥α,mα,则l∥m
D.若l⊥α,l∥m,则m⊥α
【答案】D
【解析】解:A,根据线面垂直的判定定理,要垂直平面内两条相交直线才行,不正确; B:平行于同一平面的两直线可能平行,异面,相交,不正确.
C:l∥α,mα,则l∥m或两线异面,故不正确.
D:由线面垂直的性质可知:平行线中的一条垂直于这个平面则另一条也垂直这个平面.故正确.
故选D.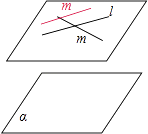
【考点精析】本题主要考查了命题的真假判断与应用和空间中直线与平面之间的位置关系的相关知识点,需要掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系;直线在平面内—有无数个公共点;直线与平面相交—有且只有一个公共点;直线在平面平行—没有公共点才能正确解答此题.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:高中数学 来源: 题型:
【题目】某学校为了了解该校学生对于某项运动的爱好是否与性别有关,通过随机抽查110名学生,得到如下![]() 的列联表:
的列联表:
喜欢该项运动 | 不喜欢该项运动 | 总计 | |
男 | 40 | 20 | 60 |
女 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由公式 ,算得
,算得![]()
附表:
| 0.025 | 0.01 | 0.005 |
| 5.024 | 6.635 | 7.879 |
参照附表,以下结论正确的是( )
A. 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
B. 在犯错语的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
C. 有99%以上的把握认为“爱好该项运动与性别无关”
D. 有99%以上的把握认为“爱好该项运动与性别有关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)求函数![]() 的单调递增区间;
的单调递增区间;
(Ⅱ)把![]() 的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移
的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象,求
的图象,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,是否存在整数
时,是否存在整数![]() ,使不等式
,使不等式![]() 恒成立?若存在,求整数
恒成立?若存在,求整数![]() 的值;若不存在,则说明理由;
的值;若不存在,则说明理由;
(3)关于![]() 的方程
的方程![]() 在
在![]() 上恰有两个相异实根,求实数
上恰有两个相异实根,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD﹣A1B1C1D1中,M,N分别是BC1 , CD1的中点,则下列说法错误的是( ) 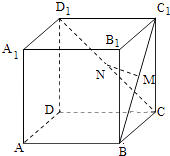
A.MN与CC1垂直
B.MN与AC垂直
C.MN与BD平行
D.MN与A1B1平行
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,连结棱长为2cm的正方体各面的中心得一个多面体容器,从顶点A处向该容器内注水,注满为止.已知顶点B到水面的高度h以每秒1cm匀速上升,记该容器内水的体积V(cm3)与时间T(S)的函数关系是V(t),则函数V(t)的导函数y=V′(t)的图象大致是( ) 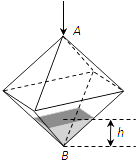
A.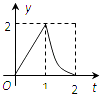
B.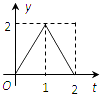
C.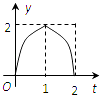
D.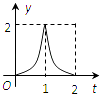
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】综合题。
(1)已知 ![]() 在区间(m2﹣4m,2m﹣2)上能取得最大值,求实数m的取值范围;
在区间(m2﹣4m,2m﹣2)上能取得最大值,求实数m的取值范围;
(2)设函数f(x)=ax﹣(k﹣1)a﹣x(a>0且a≠1)是定义域为R的奇函数,若 ![]() ,且g(x)=a2x+a﹣2x﹣2mf(x)在[1,+∞)上的最小值为﹣2,求m的值.
,且g(x)=a2x+a﹣2x﹣2mf(x)在[1,+∞)上的最小值为﹣2,求m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年9月,第22届鲁台经贸洽谈会在潍坊鲁台会展中心举行,在会展期间某展销商销售一种商品,根据市场调查,每件商品售价x(元)与销量t(万元)之间的函数关系如图所示,又知供货价格与销量呈反比,比例系数为20.(注:每件产品利润=售价﹣供货价格) 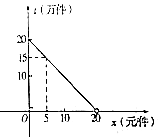
(1)求售价15元时的销量及此时的供货价格;
(2)当销售价格为多少时总利润最大,并求出最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com