
【题目】已知直线y=﹣x+1与椭圆 ![]() +
+ ![]() =1(a>b>0)相交于A、B两点.
=1(a>b>0)相交于A、B两点.
(1)若椭圆的离心率为 ![]() ,焦距为2,求线段AB的长;
,焦距为2,求线段AB的长;
(2)若向量 ![]() 与向量
与向量 ![]() 互相垂直(其中O为坐标原点),当椭圆的离心率e∈[
互相垂直(其中O为坐标原点),当椭圆的离心率e∈[ ![]() ,
, ![]() ]时,求椭圆的长轴长的最大值.
]时,求椭圆的长轴长的最大值.
【答案】
(1)解:∵ ![]() ,2c=2,
,2c=2,
∴a= ![]() ,b=
,b= ![]() ,
,
∴椭圆的方程为 ![]() .
.
联立 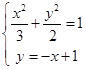 ,消去y得:5x2﹣6x﹣3=0,
,消去y得:5x2﹣6x﹣3=0,
设A(x1,y1),B(x2,y2),则 ![]() ,
, ![]() ,
,
∴|AB|= ![]()
= ![]()
![]()
= 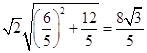 .
.
(2)设A(x1,y1),B(x2,y2),
∵ ![]() ,∴
,∴ ![]() ,
,
即x1x2+y1y2=0,
由 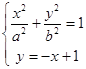 ,消去y得(a2+b2)x2﹣2a2x+a2(1﹣b2)=0,
,消去y得(a2+b2)x2﹣2a2x+a2(1﹣b2)=0,
由△=(﹣2a2)2﹣4a2(a2+b2)(1﹣b2)>0,整理得a2+b2>1
∵ ![]() ,
, ![]() ,
,
∴y1y2=(﹣x1+1)(﹣x2+1)=x1x2﹣(x1+x2)+1,
∴x1x2+y1y2=0,得:2x1x2﹣(x1+x2)+1=0,
∴ ![]() ,
,
整理得:a2+b2﹣2a2b2=0.
∴b2=a2﹣c2=a2﹣a2e2,代入上式得
2a2=1+ ![]() ,∴
,∴ ![]() ,
,
∵ ![]() ,
,
∴ ![]() ,∴
,∴ ![]() ,
,
∴ ![]() ,∴
,∴ ![]() ,
,
∴ ![]() 适合条件a2+b2>1.
适合条件a2+b2>1.
由此得 ![]() ,∴
,∴ ![]() ,
,
故长轴长的最大值为 ![]() .
.
【解析】(1)由椭圆的离心率为 ![]() ,焦距为2,求出椭圆的方程为
,焦距为2,求出椭圆的方程为 ![]() .联立
.联立 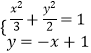 ,消去y得:5x2﹣6x﹣3=0,再由弦长公式能求求出|AB|.(2)设A(x1,y1),B(x2,y2),由
,消去y得:5x2﹣6x﹣3=0,再由弦长公式能求求出|AB|.(2)设A(x1,y1),B(x2,y2),由 ![]() ,知x1x2+y1y2=0,由
,知x1x2+y1y2=0,由 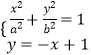 ,消去y得(a2+b2)x2﹣2a2x+a2(1﹣b2)=0,再由根的判断式得到a2+b2>1,利用韦达定理,得到a2+b2﹣2a2b2=0.由此能够推导出长轴长的最大值.
,消去y得(a2+b2)x2﹣2a2x+a2(1﹣b2)=0,再由根的判断式得到a2+b2>1,利用韦达定理,得到a2+b2﹣2a2b2=0.由此能够推导出长轴长的最大值.


科目:高中数学 来源: 题型:
【题目】已知幂函数f(x)=xa的图象经过点![]() .
.
(1)求函数f(x)的解析式,并判断奇偶性;
(2)判断函数f(x)在(﹣![]() ,0)上的单调性,并用单调性定义证明.
,0)上的单调性,并用单调性定义证明.
(3)作出函数f(x)在定义域内的大致图象(不必写出作图过程).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆Γ: ![]() =1(a>b>0)的左右焦点分别为F1 , F2 , 焦距为2c,若直线y=
=1(a>b>0)的左右焦点分别为F1 , F2 , 焦距为2c,若直线y= ![]() 与椭圆Γ的一个交点M满足∠MF1F2=2∠MF2F1 , 则该椭圆的离心率等于 .
与椭圆Γ的一个交点M满足∠MF1F2=2∠MF2F1 , 则该椭圆的离心率等于 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市出租车的现行计价标准是:路程在2 km以内(含2 km)按起步价8元收取,超过2 km后的路程按1.9 元/km收取,但超过10 km后的路程需加收50%的返空费(即单价为1.9×(1+50%)=2.85(元/km)).
(1)将某乘客搭乘一次出租车的费用f(x)(单位:元)表示为行程x(0<x≤60,单位:km)的分段函数;
(2)某乘客的行程为16 km,他准备先乘一辆出租车行驶8 km后,再换乘另一辆出租车完成余下行程,请问:他这样做是否比只乘一辆出租车完成全部行程更省钱?
(现实中要计等待时间且最终付费取整数,本题在计算时都不予考虑)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 且a1=2,an+1=2Sn+2.
(1)求数列{an}的通项公式;
(2)若数列{bn}的各项均为正数,且bn是 ![]() 与
与 ![]() 的等比中项,求bn的前n项和Tn .
的等比中项,求bn的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】濮阳市黄河滩区某村2010年至2016年人均纯收入(单位:万元)的数据如下表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(Ⅰ)求y关于x的线性回归方程;
(Ⅱ)利用(Ⅰ)中的回归方程,分析2010年至2016年该村人均纯收入的变化情况,并预测该村2017年人均纯收入.
附:回归直线的斜率和截距的最小乘法估计公式分别为: ![]() =
= 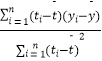 ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在底面是菱形的四棱锥P—ABCD中,∠ABC=60°,PA=AC=a,PB=PD= ![]() ,点E是PD的中点.
,点E是PD的中点.
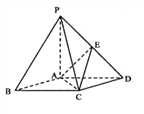
(Ⅰ)求证:PA⊥平面ABCD;
(Ⅱ)求二面角E—AC—D的大小;
(Ⅲ)求点P到平面EAC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为减少空气污染,某市鼓励居民用电(减少燃气或燃煤),采用分段计费的方法计算:电费每月用电不超过100度时,按每度0.57元计算;每月用电量超过100度时,其中的100度仍按原标准收费,超过的部分每度按0.5元计算.
(Ⅰ)设月用电![]() 度时,应交电费
度时,应交电费![]() 元,写出
元,写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(Ⅱ)小明家第一季度缴纳电费情况如下:
月份 | 一月 | 二月 | 三月 | 合计 |
交费金额 | 76元 | 63元 | 45.6元 | 184.6元 |
问小明家第一季度共用电多少度?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com