练习册

  • 练习册
  • 试题
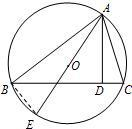
    精英家教网 > 高中数学 > 题目详情
    如图，AD是圆内接三角形ABC的高，AE是圆的直径，AB=
    		6
    ，AC=
    		3
    ，则AE×AD等于精英家教网
     
    ．
    分析：根据圆周角定理及相似三角形的判定可得到△ABE∽△ADC，根据相似三角形的边对应成比例，不难求得AE×AD的值．
    解答：解：∵AE是直径
    ∴∠ABE=∠ADC=90°
    ∵∠E=∠C
    ∴△ABE∽△ADC
    ∴
    AB
    AD
    =
    AE
    AC

    ∴AE×AD=AB•AC=3
    		2

    故答案为3
    		2
    ．
    点评：本题利用了直径对的圆周角是直角，圆周角定理，相似三角形的判定和性质求解．属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （2013•湖南模拟）如图所示，已知△ABC内接于圆O，AB是圆O的直径，四边形DCBE为平行四边形，DC⊥平面ABC，AB=2，tan∠EAB=
    		3
    2
    ．
    （1）证明：平面ACD⊥平面ADE，
    （2）令AC=x，V（x） 表示三棱锥A-CBE的体积，当V（x） 取得最大值时，求直线AD与平面ACE所成角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，已知△ABC内接于圆O，AB是圆O的直径，四边形DCBE为平行四边形，DC⊥平面ABC，AB=2，tan∠EAB=
    		3
    2
    ．
    （1）证明：平面ACD⊥平面ADE；
    （2）记AC=x，V（x）表示三棱锥A-CBE的体积，求V（x）的表达式；
    （3）当V（x）取得最大值时，求证：AD=CE．

    查看答案和解析>>

    科目：高中数学 来源：四川省双流中学2011－2012学年高二上学期期中考试数学文科试题 题型：044

    如图，已知△ABC内接于圆O，AB是圆O的直径，四边形DCBE为平行四边形，DC⊥平面ABC，AB＝2，．

    (1)证明：平面ACD⊥平面ADE；

    (2)记AC＝x求三棱锥A＝CBE的体积V(x)；

    (3)当V(x)取得最大值时，求证：AD＝CE．

    查看答案和解析>>

    科目：高中数学 来源：四川省双流中学2011－2012学年高二上学期期中考试数学理科试题 题型：044

    如图，已知△ABC内接于圆O，AB是圆O的直径，四边形DCBE为平行四边形，

    DC⊥平面ABC，AB＝2，

    (1)证明：平面ACD⊥平面ADE

    (2)记AC＝x，V(x)表示三棱锥A－CBE的体积，求V(x)的表达式；

    (3)当V(x)取得最大值时，求证：AD＝CE．

    查看答案和解析>>

    科目：高中数学 来源：2010年广东省揭阳市高考数学模拟试卷（文科）（解析版） 题型：解答题

    如图，已知△ABC内接于圆O，AB是圆O的直径，四边形DCBE为平行四边形，DC⊥平面ABC，AB=2，．
    （1）证明：平面ACD⊥平面ADE；
    （2）记AC=x，V（x）表示三棱锥A-CBE的体积，求V（x）的表达式；
    （3）当V（x）取得最大值时，求证：AD=CE．

    查看答案和解析>>

    同步练习册答案