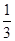练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    )在计算“1×2+2×3+…+n(n+1)”时,某同学学到了如下一种方法:先改写第k项:
    k(k+1)=[k(k+1)(k+2)-(k-1)k(k+1)],
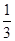    由此得1×2=(1×2×3-0×1×2),
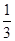    2×3=(2×3×4-1×2×3),…,
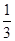    n(n+1)=[n(n+1)(n+2)-(n-1)n(n+1)].
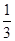    相加,得1×2+2×3+…+n(n+1)=n(n+1)(n+2).
    类比上述方法,请你计算“1×2×3+2×3×4+…+n(n+1)(n+2)”,其结果为　　　　.
    n(n+1)(n+2)(n+3)
    k(k+1)(k+2)=[k(k+1)(k+2)(k+3)-(k-1)k(k+1)(k+2)],
    ∴1×2×3+2×3×4+…+n(n+1)(n+2)=n(n+1)(n+2)(n+3).
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：填空题

    观察下列各式：是则_____________;

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    观察下列等式：
    ＋2＝4；×2＝4；＋3＝；×3＝；＋4＝；×4＝；…，根据这些等式反映的结果，可以得出一个关于自然数n的等式，这个等式可以表示为______________________．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    给出下面类比推理命题(其中Q为有理数集，R为实数集，C为复数集)：
    ①“若a，b∈R，则a－b＝0⇒a＝b”类比推出“若a，b∈C，则a－b＝0⇒a＝b”；
    ②“若a，b，c，d∈R，则复数a＋bi＝c＋di⇒a＝c，b＝d”类比推出“若a，b，c，d∈Q，则a＋b＝c＋d⇒a＝c，b＝d”；
    ③“若a，b∈R，则a－b>0⇒a>b”类比推出“若a，b∈C，则a－b>0⇒a>b”．
    其中类比得到的结论正确的个数是 (  )．
    A．0B．1C．2D．3

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    观察下列各式：55＝3 125,56＝15 625,57＝78 125，…，则52 011
    的末四位数字为  (  )．
    A．3 125B．5 625
    C．0 625D．8 125

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    有一段演绎推理是这样的:“若直线平行于平面,则该直线平行于平面内所有直线;已知直线b∥平面α,直线a?平面α,则直线b∥直线a”,结论显然是错误的,这是因为(　　)
    A．大前提错误B．小前提错误
    C．推理形式错误D．非以上错误

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    定义平面向量之间的一种运算“☉”如下:对任意的a=(m,n),b=(p,q),令a☉b=mq-np.下面说法错误的是(　　)
    A．若a与b共线,则a☉b=0
    B．a☉b=b☉a
    C．对任意的λ∈R,有(λa)☉b=λ(a☉b)
    D．(a☉b)2+(a·b)2=|a|2|b|2

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    若集合A1,A2,…,An满足A1∪A2∪…∪An=A,则称A1,A2,…,An为集合A的一种拆分.已知:
    ①当A1∪A2={a1,a2,a3}时,有33种拆分;
    ②当A1∪A2∪A3={a1,a2,a3,a4}时,有74种拆分;
    ③当A1∪A2∪A3∪A4={a1,a2,a3,a4,a5}时,有155种拆分;
    ……
    由以上结论,推测出一般结论:
    当A1∪A2∪…∪An={a1,a2,a3,…,an+1}时,有　　　　种拆分.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    挪威数学家阿贝尔曾经根据阶梯形图形的两种不同分割（如下图），利用它们的面积关系发现了一个重要的恒等式——阿贝尔公式：

    a1b1＋a2b2＋a3b3＋…＋anbn＝L1(b1－b2)＋L2(b2－b3)＋L3(b3－b4)＋…＋Ln－1(bn－1－bn)＋Lnbn，其中L1＝a1，则
    （Ⅰ）L3＝           ；
    （Ⅱ）Ln＝                 ．

    查看答案和解析>>

    同步练习册答案