
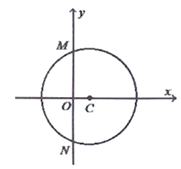
【题目】已知圆心在x轴正半轴上的圆C与直线![]() 相切,与y轴交于M,N两点,且
相切,与y轴交于M,N两点,且![]() .
.
![]() Ⅰ
Ⅰ![]() 求圆C的标准方程;
求圆C的标准方程;
![]() Ⅱ
Ⅱ![]() 过点
过点![]() 的直线l与圆C交于不同的两点D,E,若
的直线l与圆C交于不同的两点D,E,若![]() 时,求直线l的方程;
时,求直线l的方程;
![]() Ⅲ
Ⅲ![]() 已知Q是圆C上任意一点,问:在x轴上是否存在两定点A,B,使得
已知Q是圆C上任意一点,问:在x轴上是否存在两定点A,B,使得![]() ?若存在,求出A,B两点的坐标;若不存在,请说明理由.
?若存在,求出A,B两点的坐标;若不存在,请说明理由.
【答案】(I)![]() ;(II)
;(II)![]() 或
或![]() ;(III)存在
;(III)存在![]() ,
,![]() 或
或![]() ,
,![]() 满足题意.
满足题意.
【解析】
![]() 设圆C的方程为
设圆C的方程为![]() ,利用点C到直线
,利用点C到直线![]() 的距离为
的距离为![]() ,求出a,即可求圆C的标准方程;
,求出a,即可求圆C的标准方程;
![]() Ⅱ
Ⅱ![]() 设直线l的方程为
设直线l的方程为![]() 即
即![]() ,则由题意可知,圆心C到直线l的距离
,则由题意可知,圆心C到直线l的距离![]() ,即可求出k的值,
,即可求出k的值,
![]() Ⅲ
Ⅲ![]() 方法一:假设在x轴上存在两定点
方法一:假设在x轴上存在两定点![]() ,
,![]() ,设
,设![]() 是圆C上任意一点,由题意可得则
是圆C上任意一点,由题意可得则![]() ,即可求出a,b的值,
,即可求出a,b的值,
方法二:设![]() 是圆C上任意一点,由
是圆C上任意一点,由![]() 得
得![]() ,对照圆C的标准方程
,对照圆C的标准方程![]() 即
即![]() ,可得
,可得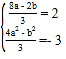 ,解得即可.
,解得即可.
解:![]() Ⅰ
Ⅰ![]() 由题意知圆心
由题意知圆心![]() ,且
,且![]() ,
,
由![]() 知
知![]() 中,
中,![]() ,
,![]() ,则
,则![]() ,
,
于是可设圆C的方程为![]()
又点C到直线![]() 的距离为
的距离为![]() ,
,
所以![]() 或
或![]() 舍
舍![]() ,
,
故圆C的方程为![]() ,
,
![]() Ⅱ
Ⅱ![]() 设直线l的方程为
设直线l的方程为![]() 即
即![]() ,则由题意可知,圆心C到直线l的距离
,则由题意可知,圆心C到直线l的距离![]() ,
,
故![]() ,解得
,解得![]() ,
,
又当![]() 时满足题意,
时满足题意,
因此所求的直线方程为![]() 或
或![]() ,
,
![]() Ⅲ
Ⅲ![]() 方法一:假设在x轴上存在两定点
方法一:假设在x轴上存在两定点![]() ,
,![]() ,设
,设![]() 是圆C上任意一点,则
是圆C上任意一点,则![]() 即
即![]() ,
,
则![]() ,
,
令![]() ,
,
解得![]() 或
或![]() ,
,
因此存在![]() ,
,![]() ,
,![]() 或
或![]() ,
,![]() 满足题意,
满足题意,
方法二:设![]() 是圆C上任意一点,
是圆C上任意一点,
由![]() 得
得![]() ,
,
化简可得![]() ,
,
对照圆C的标准方程![]() 即
即![]() ,
,
可得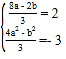 ,
,
解得解得![]() 或
或![]() ,
,
因此存在![]() ,
,![]() 或
或![]() ,
,![]() 满足题意.
满足题意.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:
【题目】“开门大吉”是某电视台推出的游戏节目.选手面对1~8号8扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.在一次场外调查中,发现参赛选手多数分为两个年龄段:20~30;30~40(单位:岁),其猜对歌曲名称与否的人数如图所示. 
(1)写出2×2列联表;判断是否有90%的把握认为猜对歌曲名称与否和年龄有关;说明你的理由;(下面的临界值表供参考) (参考公式:K2= ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)
P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 |
(2)现计划在这次场外调查中按年龄段选取6名选手,并抽取3名幸运选手,求3名幸运选手中在20~30岁之间的人数的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别是角A,B,C的对边,b= ![]() sinB,且满足tanA+tanC=
sinB,且满足tanA+tanC= ![]() . (Ⅰ)求角C和边c的大小;
. (Ⅰ)求角C和边c的大小;
(Ⅱ)求△ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx+x(x﹣a)2(a∈R),若存在 ![]() ,使得f(x)>xf'(x)成立,则实数a的取值范围是( )
,使得f(x)>xf'(x)成立,则实数a的取值范围是( )
A.![]()
B.![]()
C.![]()
D.(3,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是菱形,∠BAD=60°,AB=2,PD=![]() ,O为AC与BD的交点,E为棱PB上一点.
,O为AC与BD的交点,E为棱PB上一点.

(1)证明:平面EAC⊥平面PBD;
(2)若PD∥平面EAC,求三棱锥P-EAD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的是( )
A. 一条直线与一个平面平行,它就和这个平面内的任意一条直线平行
B. 平行于同一个平面的两条直线平行
C. 平面外的两条平行直线中的一条与一个平面平行,则另一条直线也与此平面平行
D. 与两个相交平面的交线平行的直线,必平行于这两个平面
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f (x)=a lnx+![]() +x (a≠0).
+x (a≠0).
(1)若曲线y=f (x)在点(1,f (1))处的切线与直线x-2y=0垂直,求实数a的值;
(2)讨论函数f (x)的单调性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某宾馆安排![]() 五人入住3个房间,每个房间至少住1人,且
五人入住3个房间,每个房间至少住1人,且![]() 不能住同一房间,则不同的安排方法有( )种
不能住同一房间,则不同的安排方法有( )种
A. 64 B. 84 C. 114 D. 144
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com